Урок №30. размер типов данных
Содержание:
- Вычисления с целыми числамиExplore integer math
- Вступление
- Характеристики типов с плавающей запятойCharacteristics of the floating-point types
- Определение целочисленных переменных
- Float ranges and precision
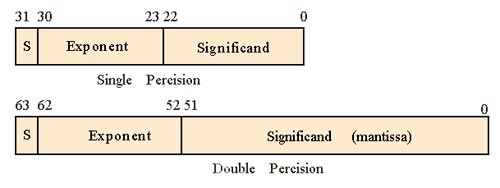
- Типы чисел с плавающей точкой (по IEEE 754)[править]
- Число половинной точности (Binary16, Half precision)править
- Число одинарной точности (Binary32, Single precision, float)править
- Число двойной точности (Binary64, Double precision, double)править
- Число четверной точности (Binary128, Quadruple precision)править
- Диапазон значений чисел с плавающей запятойправить
- Вещественные данные
- Таблицы
- Nullable-типы (нулевые типы) и операция ??
- Символы (тип char)
- Конвертация чисел в экспоненциальную запись
- What is precision?
Вычисления с целыми числамиExplore integer math
Создайте каталог с именем numbers-quickstart.Create a directory named numbers-quickstart. Сделайте его текущим, выполнив следующую команду:Make that the current directory and run the following command:
Откройте файл Program.cs в любом редакторе и замените строку следующим кодом:Open Program.cs in your favorite editor, and replace the line with the following code:
Чтобы выполнить этот код, введите в окно командной строки.Run this code by typing in your command window.
Вы увидели одну из основных математических операций с целыми числами.You’ve seen one of the fundamental math operations with integers. Тип представляет целое положительное или отрицательное число или ноль.The type represents an integer, a zero, positive, or negative whole number. Для сложения используйте символ .You use the symbol for addition. Другие стандартные математические операции с целыми числами включают:Other common mathematical operations for integers include:
- — вычитание; for subtraction
- — умножение; for multiplication
- — деление. for division
Начните с ознакомления с различными операциями.Start by exploring those different operations. Добавьте следующие строки после строки, с помощью которой записывается значение :Add these lines after the line that writes the value of :
Чтобы выполнить этот код, введите в окно командной строки.Run this code by typing in your command window.
Можно также поэкспериментировать, написав несколько математических операций в одной строке.You can also experiment by writing multiple mathematics operations in the same line, if you’d like. Например, выполните .Try for example. Допускается сочетание переменных и постоянных чисел.Mixing variables and constant numbers is allowed.
Совет
Вероятнее всего, при изучении C# (как и любого другого языка программирования) вы будете допускать ошибки в коде.As you explore C# (or any programming language), you’ll make mistakes when you write code. Компилятор найдет эти ошибки и сообщит вам о них.The compiler will find those errors and report them to you. Если результат содержит сообщения об ошибках, внимательно просмотрите пример кода и код в окне, чтобы понять, что нужно исправить.When the output contains error messages, look closely at the example code and the code in your window to see what to fix.
Это упражнение поможет вам изучить структуру кода C#.That exercise will help you learn the structure of C# code.
Вы завершили первый этап.You’ve finished the first step. Прежде чем перейти к следующему разделу, переместим текущий код в отдельный метод.Before you start the next section, let’s move the current code into a separate method. Это упростит начало работы с новым примером.That makes it easier to start working with a new example. Переименуйте метод в и запишите новый метод , который вызывает .Rename your method to and write a new method that calls . В результате ваш код должен выглядеть примерно следующим образом:When you finish, your code should look like this:
Вступление
Когда вы хотите изменить один тип данных на другой, более крупный (по размеру/диапазону), то неявное преобразование является хорошим вариантом.
Но многие начинающие программисты часто пытаются сделать что-то вроде следующего: . Однако, поскольку и являются целыми числами, никакого числового расширения не происходит. Выполняется целочисленное деление , результатом которого будет значение , которое затем неявно преобразуется в и присвоится переменной !
В случае, когда вы используете (такие как или ), замена одного или обоих целочисленных литералов значением типа с плавающей точкой ( или ) приведет к конвертации обоих операндов в значения типа с плавающей точкой и выполнится деление типа с плавающей точкой.
Но что будет, если использовать переменные? Например:
int i1 = 11;
int i2 = 3;
float x = i1 / i2;
|
1 |
inti1=11; inti2=3; floatx=i1i2; |
Значением переменной будет . Как сообщить компилятору, что мы хотим использовать деление типа с плавающей точкой вместо целочисленного деления? Правильно! Использовать один из операторов явного преобразования типов данных, чтобы указать компилятору выполнить явное преобразование.
Характеристики типов с плавающей запятойCharacteristics of the floating-point types
C# поддерживает следующие предварительно определенные типы с плавающей запятой:C# supports the following predefined floating-point types:
| Ключевое слово или тип C#C# type/keyword | Приблизительный диапазон значенийApproximate range | ТочностьPrecision | РазмерSize | Тип .NET.NET type |
|---|---|---|---|---|
| От ±1,5 x 10−45 до ±3,4 x 1038±1.5 x 10−45 to ±3.4 x 1038 | 6–9 цифр~6-9 digits | 4 байта4 bytes | System.Single | |
| от ±5,0 × 10−324 до ±1,7 × 10308±5.0 × 10−324 to ±1.7 × 10308 | 15–17 цифр~15-17 digits | 8 байт8 bytes | System.Double | |
| от ±1,0 x 10-28 до ±7,9228 x 1028±1.0 x 10-28 to ±7.9228 x 1028 | 28-29 знаков28-29 digits | 16 байт16 bytes | System.Decimal |
В приведенной выше таблице каждый тип ключевого слова C# из крайнего левого столбца является псевдонимом для соответствующего типа .NET.In the preceding table, each C# type keyword from the leftmost column is an alias for the corresponding .NET type. Они взаимозаменяемые.They are interchangeable. Например, следующие объявления объявляют переменные одного типа:For example, the following declarations declare variables of the same type:
По умолчанию все типы с плавающей запятой имеют значение .The default value of each floating-point type is zero, . Все типы с плавающей запятой имеют константы и с минимальным и максимальными итоговыми значениями этого типа.Each of the floating-point types has the and constants that provide the minimum and maximum finite value of that type. Типы и также предоставляют константы, обозначающие бесконечные и нечисловые значения.The and types also provide constants that represent not-a-number and infinity values. Например, тип предоставляет следующие константы: Double.NaN, Double.NegativeInfinity и Double.PositiveInfinity.For example, the type provides the following constants: Double.NaN, Double.NegativeInfinity, and Double.PositiveInfinity.
Так как тип характеризуется более высокой точностью и меньшим диапазоном, чем и , он подходит для финансовых расчетов.Because the type has more precision and a smaller range than both and , it’s appropriate for financial and monetary calculations.
В одном и том же выражении можно сочетать и целочисленные типы, и типы и .You can mix integral types and the and types in an expression. В этом случае целочисленные типы неявно преобразуются в один из типов с плавающей запятой. При необходимости тип неявно преобразуется в .In this case, integral types are implicitly converted to one of the floating-point types and, if necessary, the type is implicitly converted to . Выражение вычисляется следующим образом.The expression is evaluated as follows:
- Если в выражении есть тип , оно оценивается как или в реляционных сравнениях или сравнениях на равенство.If there is type in the expression, the expression evaluates to , or to in relational and equality comparisons.
- Если в выражении нет типа , оно оценивается как или в реляционных сравнениях или сравнениях на равенство.If there is no type in the expression, the expression evaluates to , or to in relational and equality comparisons.
Можно также смешивать целочисленные типы и тип в выражении.You can also mix integral types and the type in an expression. В этом случае целочисленные типы неявно преобразуются в тип , а выражение вычисляется как или в реляционных сравнениях и сравнениях на равенство.In this case, integral types are implicitly converted to the type and the expression evaluates to , or to in relational and equality comparisons.
Тип нельзя смешивать с типами и в выражении.You cannot mix the type with the and types in an expression. В этом случае, если требуется выполнить арифметические операции или операции сравнения или равенства, необходимо явно преобразовать операнды из типа или в тип , как показано в следующем примере:In this case, if you want to perform arithmetic, comparison, or equality operations, you must explicitly convert the operands either from or to the type, as the following example shows:
Можно использовать строки стандартных числовых форматов или строки пользовательских числовых форматов для форматирования значения с плавающей запятой.You can use either standard numeric format strings or custom numeric format strings to format a floating-point value.
Определение целочисленных переменных
Определение происходит следующим образом:
char c;
short int si; // допустимо
short s; // предпочтительнее
int i;
long int li; // допустимо
long l; // предпочтительнее
long long int lli; // допустимо
long long ll; // предпочтительнее
|
1 |
charc; shortintsi;// допустимо shorts;// предпочтительнее inti; longintli;// допустимо longl;// предпочтительнее longlongintlli;// допустимо longlongll;// предпочтительнее |
В то время как полные названия , и могут использоваться, их сокращенные версии (без ) более предпочтительны для использования. К тому же постоянное добавление затрудняет чтение кода (легко перепутать с именем переменной).
Float ranges and precision
In order to find the value ranges of the floating-point number in your platform, you can use the header file. This header file defines macros such as and that store the float value ranges and precision of the type.
You can also find the corresponding macros for and with the prefixes and
The following program illustrates the storage size and precision of floating-point numbers in your system.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
/* intmain() { printf(«Storage size: %d bytes\n» «Minimum float value: %E\n» «Maximum float value: %E\n» «Precision: %d decimal digits\n», sizeof(float), FLT_MIN, FLT_MAX, FLT_DIG); puts(«\nExample of float precision:\n»); doubled=12345.6; floatf=(float)d; printf(«The floating-point number d « «%18.10f\n»,d); printf(«Stored in a variable f\n» «of type float as the value « «%18.10f\n»,f); return; } |
The output of the program in our system is as follows:
|
1 2 3 4 5 6 7 8 9 10 |
Storage size4bytes Minimum floatvalue1.175494E-038 Maximum floatvalue3.402823E+038 Precision6decimal digits Example of floatprecision The floating-point numberd12345.6000000000 Stored inavariablef of type floatasthe value12345.5996093750 |
In this tutorial, we have introduced you various C float types and explained what precision means to each type of float in C.
- Was this tutorial helpful ?
Типы чисел с плавающей точкой (по IEEE 754)[править]
Число половинной точности (Binary16, Half precision)править
Число́ полови́нной то́чности — компьютерный формат представления чисел, занимающий в памяти половину машинного слова (в случае 32-битного компьютера — бит или байта). В силу невысокой точности этот формат представления чисел с плавающей запятой обычно используется в видеокартах, где небольшой размер и высокая скорость работы важнее точности вычислений.
| Знак | ||||
|---|---|---|---|---|
| Порядок | Мантисса | |||
| 1, | ||||
| 14 | 10 | 9 |
Порядок записан со сдвигом . То есть чтобы получить актуально значение порядка нужно вычесть из него сдвиг. Сдвиг можно получить по формуле , где — число бит, отведенное на хранение порядка (в случае числа половинной точности ).
Ограничения точности
- Целые от нуля до передаются как есть.
- Целые от до округляются к ближайшему чётному целому.
- Целые от до округляются до ближайшего целого, делящегося нацело на четыре.
- Целые от до округляются до ближайшего целого, делящегося на восемь.
- Целые от до округляются до ближайшего целого, делящегося на шестнадцать.
- Целые от до округляются до ближайшего целого, делящегося на тридцать два.
Число одинарной точности (Binary32, Single precision, float)править
Число́ одина́рной то́чности — компьютерный формат представления чисел, занимающий в памяти одно машинное слово (в случае 32-битного компьютера — бита или байта). Используется для работы с вещественными числами везде, где не нужна очень высокая точность.
| Знак | ||||
|---|---|---|---|---|
| Порядок (8 бит) | Мантисса (23+1 бита) | |||
| 1, | ||||
| 30 | 23 | 22 |
Порядок записан со сдвигом .
Число двойной точности (Binary64, Double precision, double)править
Число́ двойно́й то́чности —
компьютерный формат представления чисел, занимающий в памяти два машинных слова (в случае 32-битного компьютера — бита или байт). Часто используется благодаря своей неплохой точности, даже несмотря на двойной расход памяти и сетевого трафика относительно чисел одинарной точности.
| Знак | ||||
|---|---|---|---|---|
| Порядок(11 бит) | Мантисса(52+1 бит) | |||
| 1, | ||||
| 62 | 52 | 51 |
Порядок записан со сдвигом .
Число четверной точности (Binary128, Quadruple precision)править
Число́ четверно́й то́чности —
компьютерный формат представления чисел, занимающий в памяти четыре машинных слова (в случае 32-битного компьютера — бит или байт). Используется в случае необходимости крайне высокой точности.
| Знак | ||||
|---|---|---|---|---|
| Порядок(15 бит) | Мантисса(112+1 бит) | |||
| 1, | ||||
| 126 | 112 | 111 |
| Мантисса(112+1 бит) |
|---|
Порядок записан со сдвигом .
Обычно этот формат реализуется программно, случаи аппаратной реализации крайне редки. Также не гарантируется поддержка этого типа в языках программирования, хотя кое-где она и реализована (например, компилятор gcc для архитектуры x86 позволяет использовать тип __float128, являющийся программной реализацией числа с четверной точностью).
В совокупности эти факторы делают Quadruple весьма экзотичным и редко встречающимся форматом чисел с плавающей запятой.
Диапазон значений чисел с плавающей запятойправить
Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. Пара значений показателя (когда все разряды нули и когда все разряды единицы) зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся ноль, значения NaN (Not a Number, «не число», получается как результат операций типа деления нуля на ноль) и .
Данная таблица только лишь примерно указывает границы допустимых значений, без учета возрастающей погрешности с ростом абсолютного значения и существования .
| Название в IEEE 754 | Название типа переменной в Си | Диапазон значений | Бит в мантиссе | Бит на переменную |
|---|---|---|---|---|
| Half precision | — | 6,10×10-5..65504 | 11 | 16 |
| Single presicion | float | -3,4×1038..3,4×1038 | 23 | 32 |
| Double precision | double | -1,7×10308..1,7×10308 | 53 | 64 |
| Extended precision | На некоторых архитектурах (например в сопроцессоре Intel) long double | -3,4×104932..3,4×104932 | 65 | 80 |
Вещественные данные
Вещественный тип предназначен для представления действительных чисел. Вещественные числа представляются в разрядной сетке машины в нормированной форме.Нормированная форма числа предполагает наличие одной значащей цифры (не 0) до разделения целой и дробной части. Такое представление умножается на основание системы счисления в соответствующей степени. Например, число 12345,678 в нормированной форме можно представить как
12345,678 = 1,2345678·104
Число 0,009876 в нормированной форме можно представить как
0,009876 = 9,876·10-3
В двоичной системе счисления значащий разряд, стоящий перед разделителем целой и дробной части, может быть равен только 1. В случае если число нельзя представить в нормированной форме (например, число 0), значащий разряд перед разделителем целой и дробной части равен 0.
Значащие разряды числа, стоящие в нормированной форме после разделителя целой и дробной части, называются мантиссой числа.
В общем случае вещественное число в разрядной сетке вычислительной машины можно представить в виде 4 полей.
- знак — бит, определяющий знак вещественного числа (0 для положительных чисел, 1 — для отрицательных).
-
степень — определяет степень 2, на которую требуется умножить число в нормированной форме. Поскольку степень 2 для числа в нормированной форме может быть как положительной, так и отрицательной, нулевой степени 2 в представлении вещественного числа соответствует величина сдвига, которая определяется как
2n-1,
где n — количество разрядов, отводимых для представления степени числа.
- целое — бит, который для нормированных чисел всегда равен 1, поэтому в некоторых представлениях типов этот бит опущен и принимается равным 1.
- мантисса — значащие разряды представления числа, стоящие после разделителя целой и дробной части в нормированной форме.
Различают три основных типа представления вещественных чисел в языке Си:
| Тип | Обозна- чение в Си |
Кол-во бит | Биты степени | Мантисса | Сдвиг |
| простое | float | 32 | 30…23 | 22…0 | 127 |
| двойной точности | double | 64 | 62…52 | 51…0 | 1023 |
| двойной расширен- ной точности | long double | 80 | 78…64 | 62…0 | 16383 |
Как видно из таблицы, бит целое у типов float и double отсутствует. При этом диапазон представления вещественного числа состоит из двух диапазонов, расположенных симметрично относительно нуля. Например, диапазон представления чисел типа float можно представить в виде: Пример: представить число -178,125 в 32-разрядной сетке (тип float).
Пример: представить число -178,125 в 32-разрядной сетке (тип float).
Для представления числа в двоичной системе счисления преобразуем отдельно целую и дробную части:
17810 = 101100102.
0,12510 = 0,0012.
Тогда
178,12510 = 10110010,0012=1,0110010001·2111
Для преобразования в нормированную форму осуществляется сдвиг на 7 разрядов влево).
Для определения степени числа применяем сдвиг:
0111111+00000111 = 10000110.
Таким образом, число -178,125 представится в разрядной сетке как

Таблицы
наиболее точной суммыабсолютного
| Порядок | Naive | Kahan | Rump–Ogita–Oishi |
|---|---|---|---|
| ~ | 4.86 21 |
0 0 |
0 0 |
| ↑ | 4.97 14 |
0 0 |
0 0 |
| ↓ | 4.50 19 |
0 0 |
0 0 |
| Порядок | Naive | Kahan | Rump–Ogita–Oishi |
|---|---|---|---|
| ±~ | 158.96 7936 |
0 0 |
0 0 |
| ±↑ | 86.35 2560 |
0 0 |
0 0 |
| ±↓ | 175.70 11776 |
0 0 |
0 0 |
6
| Порядок | Naive | Kahan | Rump–Ogita–Oishi |
|---|---|---|---|
| ~ | 143.00 562 |
0 0 |
0 0 |
| ↑ | 126.60 473 |
0 0 |
0 0 |
| ↓ | 161.91 482 |
0 0 |
0 0 |
| ±~ | 2015.41 38889 |
0 0 |
0 0 |
| ±↑ | 1520.84 33965 |
0 0 |
0 0 |
| ±↓ | 1672.76 36513 |
0 0 |
0 0 |
6
| Порядок | Naive | Kahan | Rump–Ogita–Oishi |
|---|---|---|---|
| ~ | 4277.17 4662 |
0 0 |
0 0 |
| ↑ | 29.17 111 |
0 0 |
0 0 |
| ↓ | 7508.68 7915 |
0 0 |
0 0 |
| ±~ | 475.68 8221 |
1.09 21 |
0 0 |
| ±↑ | 65.39 861 |
0.01 1 |
0 0 |
| ±↓ | 270.34 1736 |
0 0 |
0 0 |
о
| Порядок | Naive | Kahan | Rump–Ogita–Oishi |
|---|---|---|---|
| ~ | 4.84 19 |
0.01 1 |
0 0 |
| ↑ | 2.81 11 |
0.01 1 |
0 0 |
| ↓ | 6.53 26 |
0 0 |
0 0 |
| ±~ | 33.83 1650 |
1.26 23 |
0 0 |
| ±↑ | 12.76 422 |
0.31 6 |
0 0 |
| ±↓ | 18.54 548 |
0 0 |
0 0 |
| Порядок | Naive | Kahan | Rump–Ogita–Oishi |
|---|---|---|---|
| ~ | 17.77 483 |
1.46 61 |
0 0 |
| ↑ | 10.92 243 |
0.34 19 |
0 0 |
| ↓ | 19.71 734 |
0 0 |
0 0 |
| Порядок | Всё подряд | Отдельно + и – |
|---|---|---|
| ±~ | 78.65 2336 |
2121.61 50048 |
| ±↑ | 76.27 2496 |
2465.55 66432 |
| ±↓ | 52.74 480 |
2863.61 99200 |
6
| Порядок | Naive | Kahan | Rump–Ogita–Oishi |
|---|---|---|---|
| ~ | 210 | 522 | |
| ↑ | 410 | ||
| ↓ | 42 |
для себя
- Если нужно испортить сумму, получаемую наивным алгоритмом, то можно складывать отдельно положительные и отдельно отрицательные числа. Иногда, но не всегда, сортировка чисел по убыванию модуля также «ломает» наивный алгоритм, лучше сортировать по возрастанию, но и это в ряде случаев даёт более плохой результат, чем в случае хаотичного порядка.
- Если нужно получить ожидаемо хороший результат, следует взять алгоритм Rump–Ogita–Oishi, я не нашёл случайных тестов, при которых он выдавал бы не наиболее точную сумму. Недостаток алгоритма в том, что работать он будет медленнее наивного сложения. Ускорить такой алгоритм, вероятно, можно, пользуясь битовым представлением числа с плавающей запятой и кое-какими трюками, но у нас такой задачи на этот обзор не было.
- Алгоритм Кэхэна значительно лучше наивного суммирования и гораздо проще алгоритма Rump–Ogita–Oishi, поэтому наиболее целесообразен на практике, где точность наивного метода вам не подходит. Просто убедитесь заранее, что ваши числа не обладают какими-то экстраординарными свойствами, которые «завалят» данный алгоритм.
- Наивное суммирование в общем-то не такое страшное, как могло показаться. Ну, подумаешь, потеряли мы 5 десятичных цифр (если N не более миллиона). Много? Если их у вас 16, то вроде бы не страшно, а если 7 (для float), то вроде бы… хотя, друзья, неужели кто-то будет складывать миллион чисел в типе float? Вы серьёзно? Это допустимо только если вам нужна одна правильная цифра, либо если массив обладает какой-то особой спецификой, и то я бы не рискнул.
- Это творческий процесс, я создал свою субъективную схему тестирования и не считаю это научно-достоверным знанием, а потому не выношу на суд общественности. Коды алгоритмов я дал выше, если вам очень нужно, то не составит труда написать своё сравнение алгоритмов и получить свои данные.
- Мой код не автоматизирован, чтобы его запускать для получения разных тестов, нужно ковыряться в программе и менять какие-то параметры, это просто неприлично — давать такой код. А написание полноценной системы тестирования в задачи публикации не входило.
Nullable-типы (нулевые типы) и операция ??
Объявление и инициализация Nullable-переменных
В работе с типами-значениями есть одна особенность, они не могут иметь значение null. При наличии любой из следующих строк кода, компиляция программы не будет выполнена:
int nv = null; bool bv = null;
На практике, особенно при работе с базами данных, может возникнуть ситуация, когда в записи из таблицы пропущены несколько столбцов (нет данных), в этом случае, соответствующей переменной нужно будет присвоить значение null, но она может иметь тип int или double, что приведет к ошибке.
Можно объявить переменную с использованием символа ? после указания типа, тогда она станет nullable-переменной – переменной поддерживающей null-значение:
int? nv1 = null; bool? bv1 = null;
Использование символа ? является синтаксическим сахаром для конструкции Nullable<T>, где T – это имя типа. Представленные выше примеры можно переписать так:
Nullable<int> nv1 = null; Nullable<bool> bv1 = null;
Проверка на null. Работа с HasValue и Value
Для того чтобы проверить, что переменная имеет значение null можно воспользоваться оператором is с шаблоном типа:
bool? flagA = true;
if(flagA is bool valueOfFlag)
{
Console.WriteLine("flagA is not null, value: {valueOfFlag}");
}
Также можно воспользоваться свойствами класса Nullable
-
Nullable<T>.HasValue
Возвращает true если переменная имеет значение базового типа. То есть если она не null.
-
Nullable<T>.Value
Возвращает значение переменной если HasValue равно true, иначе выбрасывает исключение InvalidOperationException.
bool? flagB = false;
if(flagB.HasValue)
{
Console.WriteLine("flagB is not null, value: {flagB.Value}");
}
Приведение Nullable-переменной к базовому типу
При работе с Nullable-переменными их нельзя напрямую присваивать переменным базового типа. Следующий код не будет скомпилирован:
double? nvd1 = 12.3; double nvd2 = nvd1; // error
Для приведения Nullable-переменной к базовому типу можно воспользоваться явным приведением:
double nvd3 = (double) nvd1;
В этом случае следует помнить, что если значение Nullable-переменной равно null, то при выполнении данной операции будет выброшено исключение InvalidOperationException.
Второй вариант – это использование оператора ??, при этом нужно дополнительно задаться значением, которое будет присвоено переменной базового типа если в исходной лежит значение null
double nvd4 = nvd1 ?? 0.0; Console.WriteLine(nvd4); bool? nvb1 = null; bool nvb2 = nvb1 ?? false; Console.WriteLine(nvb1); Console.WriteLine(nvb2);
Второй вариант позволяет более лаконично обрабатывать ситуацию, когда вызов какого-то метода может возвращать null, а результат его работы нужно присвоить типу-значению, при этом заранее известно, какое значение нужно присвоить переменной в этой ситуации:
static int? GetValue(bool flag)
{
if (flag == true)
return 1000;
else
return null;
}
static void Main(string[] args)
{
int test1 = GetValue(true) ?? 123;
Console.WriteLine(test1);
int test2 = GetValue(false) ?? 123;
Console.WriteLine(test2);
}
Символы (тип char)
Для хранения символов Java использует специальный тип char. Он отличается от типа char в языках C/C++, где представляет собой целочисленный тип с размером 8 бит. В Java для char используется кодировка Unicode и для хранения Unicode-символов используется 16 бит или 2 байта. Диапазон допустимых значений — от 0 до 65536 (отрицательных значений не существует).
Из примера выше видно, что переменной можно присвоить код символа или непосредственно сам символ, который следует окружить одинарными кавычками. Попробуйте запустить пример и посмотреть, какое слово получится из трёх указанных символов.
Не следует путать символ ‘a’ со строкой «a», состоящей из одного символа. На экране монитора они выглядят одинаково, но в программах ведут себя по разному.
Стандартные символы ASCII можно выводить сразу. Если нужно вывести специальный символ из Unicode, то можно воспользоваться шестнадцатеричным представлением кода в escape-последовательности — вы указываете обратную наклонную черту и четыре цифры после u. Например:
Хотя тип char используется для хранения Unicode-символов, его можно использовать как целочисленный тип, используя сложение или вычитание.
В результате получим:
Если вы думаете, что увеличив значение переменной ch1 ещё на одну единицу, получите символ «й», то глубоко заблуждаетесь.
Чтобы узнать, какой символ содержится в значении переменной, заданной как int, можно воспользоваться двумя специальными методами из класса EncodingUtils:
Для стандартных символов ASCII:
Для расширенной таблицы символов:
Методы работают со строками, но если мы используем строку из одного символа, то получим то, что нам нужно.
В упрощённом виде, если работаем со стандартными символами ASCII (on 0 до 127), то можно получить символ из int ещё проще.
Класс Character
Класс Character является оболочкой вокруг типа char. Чтобы получить значение типа char, содержащее в объекте класса Character, вызовите метод charValue().
С классом Character редко имеют дело в Android, но помните, что класс содержит огромное количество констант и методов. Например, можно определить, является ли символ цифрой или буквой, или написан ли символ в нижнем или в верхнем регистре.
Конвертация чисел в экспоненциальную запись
Для конвертации чисел в экспоненциальную запись необходимо следовать процедуре, указанной ниже:
Ваш экспонент начинается с нуля.
Переместите разделительную точку (которая разделяет целую и дробную части) влево, чтобы слева от нее осталась только одна ненулевая цифра:
каждое перемещение точки влево увеличивает экспонент на ;
каждое перемещение точки вправо уменьшает экспонент на .
Откиньте все нули перед первой ненулевой цифрой в целой части.
Откиньте все конечные нули в правой (дробной) части, только если исходное число является целым (без разделительной точки).
Рассмотрим примеры:
Самое главное, что нужно запомнить — это то, что цифры в мантиссе (часть перед ) называются значащими цифрами. Количество значащих цифр определяет точность самого значения. Чем больше цифр в мантиссе, тем точнее значение.
What is precision?
If you consider the fraction 5/3, this number can be represented in decimal as with infinite 6. When you use the floating-point type with limited bytes to store infinite number, it is impossible. Therefore the floating-point value can be stored only with a limited precision. The precision is expressed as a number of significant digits or in another way, the precision is defined as how many digits that a number can represent without data loss.
For example, the type with 4 bytes = 4 x 8 bits = 32 bits, is for numbers with single precision. It means that a float gives 1 sign bit, 8 bits of exponent and 23 bits of significand.
The type is for a number with the double precision that gives 1 sign bit, 11 bits of exponent and 52 bits of significand. (8 bytes x 8 bits = 64 bits = 1 bits + 52 bits + 11 bits).