Метод корреляционного анализа: пример. корреляционный анализ — это
Содержание:
- Прочитайте журнал событий
- Пример применения метода корреляционного анализа
- Коэффициент корреляции частный, его значения
- § 8. Методика вычисления выборочного коэффициента корреляции
- Памятка
- Предвзятость средств массовой информации
- 9.1.3. Простая линейная регрессия
- Литература
- Множественная корреляция, её коэффициент
- Hard Reset средствами самой системы Android
- Индекс множественной корреляции
- Критерии и методы
- КРИТЕРИЙ СПИРМЕНА
- Суть корреляционного анализа
- Оценка
- Корреляционный анализ
Прочитайте журнал событий
В июне 2020 года Microsoft исправила Windows 10 для защиты от уязвимости безопасности Bluetooth. Однако это привело к проблемам с подключением некоторых устройств Bluetooth.
Вы можете увидеть, влияет ли это на вас. Нажмите клавишу Windows + X и нажмите «Просмотр событий». Под сводкой административных событий разверните Ошибка и найдите следующее:
- Код события: 22
- Источник события : BTHUSB или BTHMINI
- Имя: BTHPORT_DEBUG_LINK_KEY_NOT_ALLOWED
- Текст сообщения о событии: Ваше устройство Bluetooth попыталось установить отладочное соединение. Стек Windows Bluetooth не разрешает отладочное соединение, пока оно не находится в режиме отладки.
Если вы видите это, Microsoft рекомендует связаться с производителем вашего устройства Bluetooth, чтобы узнать, сделали ли они патч. Если нет, вам может потребоваться купить новое устройство Bluetooth полностью.
Пример применения метода корреляционного анализа
В Великобритании было предпринято любопытное исследование. Оно посвящено связи курения с раком легких, и проводилось путем корреляционного анализа. Это наблюдение представлено ниже.
|
Профессиональная группа |
курение |
смертность |
|
Фермеры, лесники и рыбаки |
77 |
84 |
|
Шахтеры и работники карьеров |
137 |
116 |
|
Производители газа, кокса и химических веществ |
117 |
123 |
|
Изготовители стекла и керамики |
94 |
128 |
|
Работники печей, кузнечных, литейных и прокатных станов |
116 |
155 |
|
Работники электротехники и электроники |
102 |
101 |
|
Инженерные и смежные профессии |
111 |
118 |
|
Деревообрабатывающие производства |
93 |
113 |
|
Кожевенники |
88 |
104 |
|
Текстильные рабочие |
102 |
88 |
|
Изготовители рабочей одежды |
91 |
104 |
|
Работники пищевой, питьевой и табачной промышленности |
104 |
129 |
|
Производители бумаги и печати |
107 |
86 |
|
Производители других продуктов |
112 |
96 |
|
Строители |
113 |
144 |
|
Художники и декораторы |
110 |
139 |
|
Водители стационарных двигателей, кранов и т. д. |
125 |
113 |
|
Рабочие, не включенные в другие места |
133 |
146 |
|
Работники транспорта и связи |
115 |
128 |
|
Складские рабочие, кладовщики, упаковщики и работники разливочных машин |
105 |
115 |
|
Канцелярские работники |
87 |
79 |
|
Продавцы |
91 |
85 |
|
Работники службы спорта и отдыха |
100 |
120 |
|
Администраторы и менеджеры |
76 |
60 |
|
Профессионалы, технические работники и художники |
66 |
51 |
Начинаем корреляционный анализ. Решение лучше начинать для наглядности с графического метода, для чего построим диаграмму рассеивания (разброса).
Она демонстрирует прямую связь. Однако на основании только графического метода сделать однозначный вывод сложно. Поэтому продолжим выполнять корреляционный анализ. Пример расчета коэффициента корреляции представлен ниже.
С помощью программных средств (на примере MS Excel будет описано далее) определяем коэффициент корреляции, который составляет 0,716, что означает сильную связь между исследуемыми параметрами. Определим статистическую достоверность полученного значения по соответствующей таблице, для чего нам нужно вычесть из 25 пар значений 2, в результате чего получим 23 и по этой строке в таблице найдем r критическое для p=0,01 (поскольку это медицинские данные, здесь используется более строгая зависимость, в остальных случаях достаточно p=0,05), которое составляет 0,51 для данного корреляционного анализа. Пример продемонстрировал, что r расчетное больше r критического, значение коэффициента корреляции считается статистически достоверным.
Коэффициент корреляции частный, его значения
Частные коэффициенты корреляции используются для отслеживания взаимосвязи изменения величины от множества факторов. Можно сказать, то частный коэффициент показывает степень тесноты связи в случае, когда все остальные признаки исключены из рассматриваемого множества.
Частые коэффициенты могут применяться при отборе факторов воздействия, определении степени их значимости при воздействии на изучаемый объект. Для этих целей строится уравнение репрессии, которое отслеживает факторы по размеру их коэффициента. На каждом шаге исключается частный корреляционный коэффициент с наименьшим значением.
Перед применением частных коэффициентов множество данных тестируется на установление линейных связей. Если связи отсутствуют, то далее осуществляет анализ связи исследуемого объекта и факторов. Частные коэффициенты взаимосвязей позволяют сопоставить взаимное влияние величин и факторов друг на друга для общих отношений и частных соприкосновений.
Значения частного коэффициента корреляции означают следующее:
- Если R = 0, то взаимосвязь нейтральная, влияния нет.
- Значение коэффициента в промежутке от 0,09 до 0,19 говорит о незначительной слабой связи.
- Слабая связь устанавливается в диапазоне от 0,19 до 0,49
- Средняя взаимосвязь от 0,49 до 0,69
- Сильная связь от 0,69 до 0, 99.
Замечание 2
Частный коэффициент корреляции применяется в эконометрике для того, чтобы отслеживать изменение экономического процесса или явления под воздействием внутренних и внешних факторов.
§ 8. Методика вычисления выборочного коэффициента корреляции
Пусть требуется
по данным корреляционной таблицы
вычислить выборочный коэффициент
корреляции. Можно значительно упростить
расчет, если перейти к условным вариантам
(при этом величина rв
не изменится)
ui=(xi—С1)/h1
и υj=(yj—С2)/h2.
В этом случае
выборочный коэффициент корреляции
вычисляют по формуле
 .
.
Величины u,
υ

и 
можно найти методом произведений (см.
гл. XVII, § 4), а при малом числе данных—
непосредственно исходя из определений
этих величин. Остается указать способ
вычисления  ,
,
где  —
—
частота пары
условных вариант (u,
υ).
Можно доказать,
что справедливы формулы (см. пояснение
в конце параграфа):
 ,
,
где
 ,
,
 ,
,
где
 .
.
Для контроля
целесообразно выполнить расчеты по
обеим формулам и сравнить результаты;
их совпадение свидетельствует о
правильности вычислений.
Покажем на примере,
как пользоваться приведенными формулами.
Пример 1.
Вычислить ^ «по»» П0
данным корреляционной табл. 14.
Таблица 14
|
Y |
X |
ny |
|||||
|
10 |
20 |
30 |
40 |
50 |
60 |
||
|
15 |
5 |
7 |
— |
— |
— |
— |
12 |
|
25 |
— |
20 |
23 |
— |
— |
— |
43 |
|
35 |
— |
— |
30 |
47 |
2 |
— |
79 |
|
45 |
— |
— |
10 |
11 |
20 |
6 |
47 |
|
55 |
— |
— |
— |
9 |
7 |
3 |
19 |
|
nx |
5 |
27 |
63 |
67 |
29 |
9 |
n=200 |
Решение. Перейдем
к условным вариантам: ui=(xi—С1)/h1
= = (xi
—40)/10 (в качестве
ложного нуля С1
взята варианта х=40.
расположенная
примерно в середине вариационного ряда;
шаг h1
равен разности
между двумя соседними вариантами: 20—10
= 10) и υj=(yj—С2)/h2
= (yj
—35)/10 (в качестве
ложного нуля С2
взята варианта у =35, расположенная в
середине вариационного ряда; шаг h2
равен разности между двумя соседними
вариантами: 25—15=10).
Составим
корреляционную таблицу в условных
вариантах. Практически это делают так:
в первом столбце вместо ложного нуля
С2
(варианты 35) пишут 0; над нулем последовательно
записывают —1,
—2; под нулем пишут 1, 2. В первой строке
вместо ложного нуля С1
(варианты 40) пишут 0; слева от нуля
последовательно записывают —1, —2, —3;
справа от нуля пишут 1, 2. Все остальные
данные переписывают из первоначальной
корреляционной таблицы. В итоге получим
корреляционную табл. 15 в условных
вариантах.
Таблица
15
|
υ |
u |
nυ |
|||||
|
-3 |
-2 |
— 1 |
1 |
2 |
|||
|
—2 |
5 |
7 |
— |
— |
— |
— |
12 |
|
—1 |
— |
20 |
23 |
— |
— |
— |
43 |
|
— |
— |
30 |
47 |
2 |
— |
79 |
|
|
1 |
— |
— |
10 |
11 |
20 |
6 |
47 |
|
2 |
— |
— |
— |
9 |
7 |
3 |
19 |
|
nu |
5 |
27 |
63 |
67 |
29 |
9 |
n = |
Теперь для вычисления
искомой суммы  составим
составим
расчетную табл. 16. Пояснения к составлению
табл. 16:
1. В каждой клетке,
в которой частота nuυ
≠ 0, записывают
в правом верхнем углу произведение
частоты nuυ
на варианту u.
Например, в
правых верхних углах клеток первой
строки записаны произведения: 5·(—3) =
—15; 7·(—2) = —14.
2. Складывают все
числа, помещенные в правых верхних углах
клеток одной строки и их сумму записывают
в клетку этой же строки столбца u.
Например, для первой строки
U
== —15+(—14)= —29.
3. Умножают варианту
υ
на U
и полученное произведение заци-сывают
в последнюю клетку той же строки, т. е.
в клетку столбца υU.
Например,
в первой строке таблицы υ
= —2,
U
= —29; следовательно, υU
= (—2)·(—29) = 58.
4. Наконец, сложив
все числа столбца υU,
получают сумму
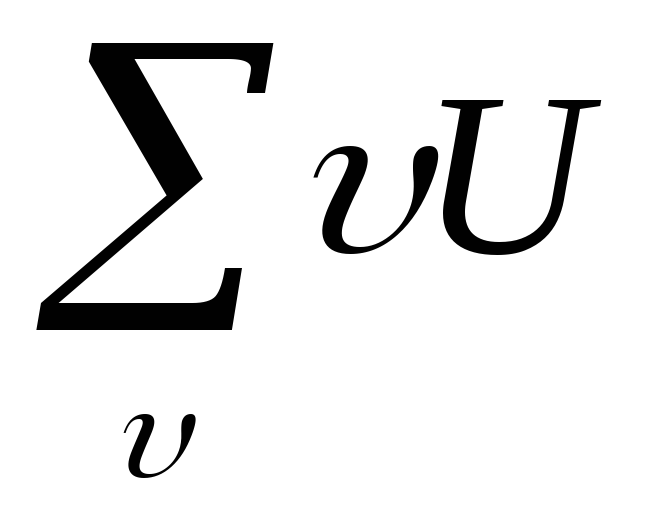 ,
,
которая равна искомой сумме  .
.
Например, для табл.
16 имеем
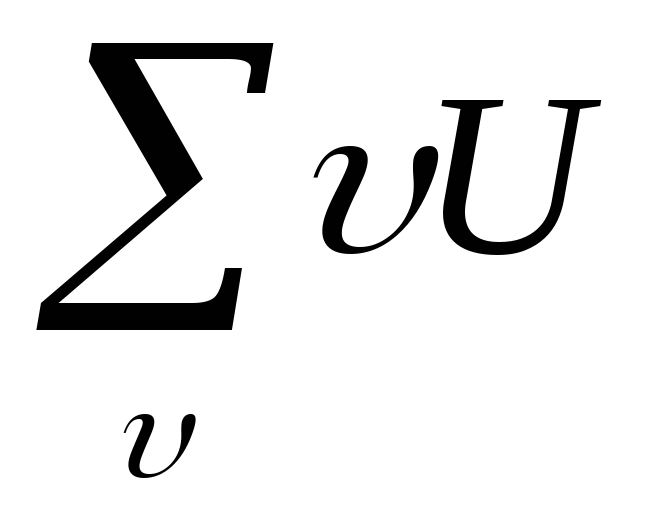 =
=
169; следовательно, искомая сумма  =
=
169.
Таблица 16
|
υ |
u ч 1 |
U= = |
υU |
|||||
|
-3 |
-2 |
—1 |
1 |
2 |
||||
|
-2 |
—15 5 -10 |
-14 7 -14 |
— |
— |
— |
— |
—29 |
58 |
|
-1 |
— |
—40 20 -20 |
—23 23 —23 |
— |
— |
— |
-63 |
63 |
|
— |
— |
-30 30 |
47 |
2 2 |
— |
—28 |
||
|
1 |
— |
— |
—10 10 10 |
11 11 |
20 20 20 |
12 6 6 |
22 |
22 |
|
2 |
— |
— |
— |
9 18 |
7 7 14 |
6 3 6 |
13 |
26 |
|
V= = |
—10 |
-34 |
—13 |
29 |
34 |
12 |
|
|
|
uV |
30 |
68 |
13 |
34 |
« |
|
Контроль |
Для контроля
аналогичные вычисления производят по
столбцам:
произведения nuυυ
записывают в левый нижний угол клетки,
содержащей частоту nuυυ
≠ 0; все числа,
помещенные в левых нижних углах клеток
одного столбца, складывают и их сумму
записывают в строку V;
далее умножают каждую варианту u
на V
и результат записывают в клетках
последней строки.
Наконец, сложив
все числа последней строки, получают
сумму
 ,
,
которая также равна искомой сумме  .
.
Например, для табл.
16 имеем
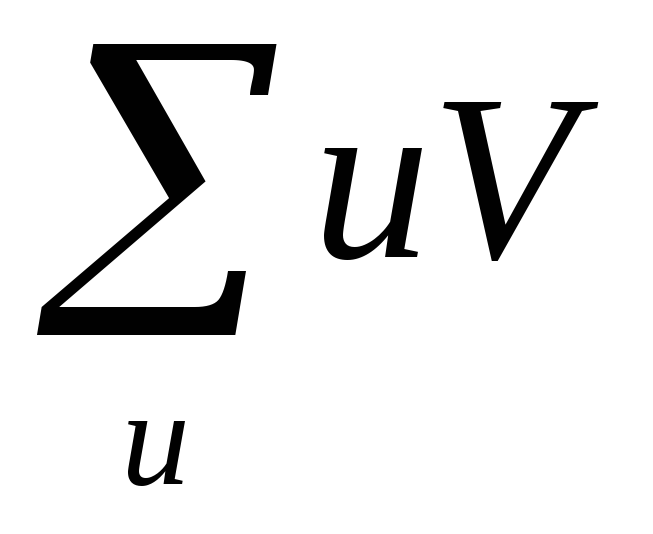 =
=
169; следовательно, = 169.
= 169.
Теперь, когда мы
научились вычислять  ,
,
приведем пример на отыскание выборочного
коэффициента корреляции.
Памятка
- Корреляция – это соотношение, взаимозависимость нескольких переменных.
- Связь бывает положительной и отрицательной.
- Коэффициент корреляции определяет степень взаимозависимости одной переменной от другой.
- На основании корреляции люди выдвигают гипотезы (часто ошибочные).
- Истинная причина корреляции порою скрыта под множеством факторов и внешних сил.
- Бывает ложная корреляционная зависимость.
- Раскладывая яйца по корзинам, помните о том, что они не должны коррелироваться друг с другом.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Использую для заработка
Предвзятость средств массовой информации
Рассмотрим, как наличие корреляционной связи может быть неправильно истолковано. Группу британских студентов, отличающихся плохим поведением, опросили относительно того, курят ли их родители. Потом тест опубликовали в газете. Результат показал сильную корреляцию между курением родителей и правонарушениями их детей. Профессор, который проводил это исследование, даже предложил поместить на пачки сигарет предупреждение об этом. Однако существует целый ряд проблем с таким выводом. Во-первых, корреляция не показывает, какая из величин является независимой. Поэтому вполне можно предположить, что пагубная привычка родителей вызвана непослушанием детей. Во-вторых, нельзя с уверенностью сказать, что обе проблемы не появились из-за какого-то третьего фактора. Например, низкого дохода семей. Следует отметить эмоциональный аспект первоначальных выводов профессора, который проводил исследование. Он был ярым противником курения. Поэтому нет ничего удивительного в том, что он интерпретировал результаты своего исследования именно так.
9.1.3. Простая линейная регрессия
Применение линейного регрессионного анализа имеет специфические черты по сравнению с другими методами обработки данных. Его непосредственное употребление ограничено, в основном, задачами о предсказании значений зависимой переменной по известным значениям аргумента (или аргументов), что в психологии задача не слишком востребованная. Однако, во-первых, линейная регрессия входит как часть во многие другие методы (например, анализ медиации и модерации, о которых речь пойдет в следующей главе), и, во-вторых, служит простым примером отыскания наилучших параметров для модели определенного типа, и психологу полезно понимать суть этого метода. Качество каждого набора параметров, а затем и модели в целом, оценивается процентом дисперсии, который остался вне предсказаний, сделанных моделью по данным значениям аргументов. Замечательным результатом для читателя будет здесь улавливание аналогий с двухфакторным дисперсионным анализом.
Литература
- Гмурман В. Е.<span title=»Статья «Гмурман, Владимир Ефимович» в русском разделе отсутствует»>ru</span>uk. Теория вероятностей и математическая статистика: Учебное пособие для вузов. — 10-е издание, стереотипное. — Москва: Высшая школа, 2004. — 479 с. — ISBN 5-06-004214-6.
- Елисеева И. И., Юзбашев М. М. Общая теория статистики: Учебник / Под ред. И. И. Елисеевой. — 4-е издание, переработанное и дополненное. — Москва: Финансы и Статистика, 2002. — 480 с. — ISBN 5-279-01956-9.
- Общая теория статистики: Учебник / Под ред. Р. А. Шмойловой. — 3-е издание, переработанное. — Москва: Финансы и Статистика, 2002. — 560 с. — ISBN 5-279-01951-8.
- Суслов В. И., Ибрагимов Н. М., Талышева Л. П., Цыплаков А. А. Эконометрия. — Новосибирск: СО РАН, 2005. — 744 с. — ISBN 5-7692-0755-8.
Множественная корреляция, её коэффициент
Множественная корреляция — это вероятностная зависимость между одной величиной с
одной стороны, и одновременно несколькими другими ,
с другой стороны.
То есть, в отличие от парной корреляции, при которой
на изменения зависимой (результирующей) переменной влияет одна независимая (объясняющая) переменная,
при множественной корреляции независимых (объясняющих) переменных две или больше.
Цель корреляционного анализа в случае множественной корреляции — установить, есть ли зависимость между
переменными и насколько тесно связаны между собой зависимая переменная, с одной стороны, и независимые
переменные, с другой стороны, и зависят ли друг от друга независимые переменные .
Для того чтобы можно было бы применять модель множественной линейной регрессии, прежде, при анализе
множественной корреляции должны быть установлены следующие факты:
- зависимая переменная тесно зависит от независимых переменных (тесноту связи, как и в случае
парной корреляции, показывают ); - нет тесной зависимости между независимыми переменными.
Коэффициент множественной корреляции в случае двухфакторной корреляции рассчитывается по следующей формуле:
.
Коэффициенты множественной корреляции между зависимой переменной
и независимыми переменными
записываются в корреляционную матрицу:
Пример 1. Аналитик предприятия решил проверить факторы, которые
влияют на размер заработной платы сотрудников . Предварительно
в качестве объясняющих факторов выбраны: возраст сотрудника ,
стаж работы , оценка теста для приёма
на работу и число подчинённых
сотрудников . Случайно были выбраны
200 сотрудников, данные которых были обобщены. В результате была получена следующая корреляционная матрица:
| 1 | |||||
| -0,27 | 1 | ||||
| 0,78 | -0,63 | 1 | |||
| -0,83 | 0,47 | -0,89 | 1 | ||
| 0,65 | -0,46 | 0,17 | -0,21 | 1 |
Установить, какие переменные можно выбрать как независимые, для того, чтобы далее
можно было бы строить модель множественной регрессии.
Решение.
Корреляционная матрица показывает, что между переменными:
- и — слабая линейная связь: -0,27;
- и — средне тесная положительная линейная связь: 0,78;
- и — тесная отрицательная линейная связь: -0,83;
- и — средне тесная линейная связь: 0,65;
- и — тесная отрицательная линейная связь: -0,89;
- и — слабая линейная связь: 0,17;
- и — слабая линейная связь: -0,21.
Таким образом, не следует включать в число переменных, влияющих на размер заработной
платы возраст сотрудников . Так как
между независимыми переменными и
установлена тесная отрицательная связь,
не включаем в число переменных, влияющих на размер заработной платы стаж работы .
Выбираем в качестве независимых переменных оценку теста для приёма
на работу и число подчинённых
сотрудников .
Чтобы установить тесноту связи между заработной платой сотрудников ,
с одной стороны, и оценкой теста для приёма
на работу и числом подчинённых
сотрудников , с другой стороны,
вычислим коэффициент множественной (двухфакторной) корреляции:
Таким образом, между заработной платой сотрудников, с одной стороны, и
оценкой теста для приёма на работу и числом подчинённых, с другой стороны, существует тесная линейная
связь.
Как показывает пример выше, в исследованиях поведения человека,
как и во многих других направлениях, важно установить, какие факторы из многих действительно влияют на
результат при учете влияния всех остальных факторов
Hard Reset средствами самой системы Android
Индекс множественной корреляции
 22табл
22табл
4. Оценка значения результативного признака при заданных значениях факторов. Y(0.0,0.0,) = -32.24 + 0.2412 * 0.0 + 0.1151 * 0.0 = -32.24
Доверительные интервалы с вероятностью 0.95 для индивидуального значения результативного признака. S2 =
XT(XTX)-1Xгде XT =
(XTX)-1
| 5.8295 | -0.0116 | -0.0002 |
| -0.0116 | 0.0001 | -0 |
| -0.0002 | -0 |
2YY
5. Проверка гипотез относительно коэффициентов уравнения регрессии (проверка значимости параметров множественного уравнения регрессии).
1) t-статистика Статистическая значимость коэффициента регрессии b подтверждается
Статистическая значимость коэффициента регрессии b1 подтверждается Статистическая значимость коэффициента регрессии b2 подтверждается
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими: (bi — t i Si; bi + t i S i) b : (-44.2749;-20.2039)
b 1: (0.204;0.2784) b 2: (0.0887;0.1415)
2) F-статистика. Критерий Фишера Fkp = 4.35 Поскольку F > Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно
6. Проверка на наличие гетероскедастичности методом графического анализа остатков. В этом случае по оси абсцисс откладываются значения объясняющей переменной Xi, а по оси ординат квадраты отклонения ei2.
| y | y(x) | e=y-y(x) | e2 |
| 130.34 | 131.53 | -1.19 | 1.43 |
| 126.83 | 132.94 | -6.11 | 37.35 |
| 108.61 | 105.5 | 3.11 | 9.67 |
| 116.01 | 112.67 | 3.34 | 11.16 |
| 135.44 | 132.68 | 2.76 | 7.63 |
| 142.88 | 149.54 | -6.66 | 44.39 |
| 158.69 | 151.81 | 6.88 | 47.28 |
| 168.49 | 170.91 | -2.42 | 5.87 |
| 174.8 | 178.48 | -3.68 | 13.56 |
| 187.15 | 174.63 | 12.52 | 156.86 |
Критерии и методы
КРИТЕРИЙ СПИРМЕНА
Коэффициент ранговой корреляции Спирмена – это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.
Чарльз Эдвард Спирмен
1. История разработки коэффициента ранговой корреляции
Данный критерий был разработан и предложен для проведения корреляционного анализа в 1904 году Чарльзом Эдвардом Спирменом, английским психологом, профессором Лондонского и Честерфилдского университетов.
2. Для чего используется коэффициент Спирмена?
Коэффициент ранговой корреляции Спирмена используется для выявления и оценки тесноты связи между двумя рядами сопоставляемых количественных показателей. В том случае, если ранги показателей, упорядоченных по степени возрастания или убывания, в большинстве случаев совпадают (большему значению одного показателя соответствует большее значение другого показателя — например, при сопоставлении роста пациента и его массы тела), делается вывод о наличии прямой корреляционной связи. Если ранги показателей имеют противоположную направленность (большему значению одного показателя соответствует меньшее значение другого — например, при сопоставлении возраста и частоты сердечных сокращений), то говорят об обратной связи между показателями.
- Коэффициент корреляции Спирмена обладает следующими свойствами:
- Коэффициент корреляции может принимать значения от минус единицы до единицы, причем при rs=1 имеет место строго прямая связь, а при rs= -1 – строго обратная связь.
- Если коэффициент корреляции отрицательный, то имеет место обратная связь, если положительный, то – прямая связь.
- Если коэффициент корреляции равен нулю, то связь между величинами практически отсутствует.
- Чем ближе модуль коэффициента корреляции к единице, тем более сильной является связь между измеряемыми величинами.
3. В каких случаях можно использовать коэффициент Спирмена?
В связи с тем, что коэффициент является методом непараметрического анализа, проверка на нормальность распределения не требуется.
Сопоставляемые показатели могут быть измерены как в непрерывной шкале (например, число эритроцитов в 1 мкл крови), так и в порядковой (например, баллы экспертной оценки от 1 до 5).
Эффективность и качество оценки методом Спирмена снижается, если разница между различными значениями какой-либо из измеряемых величин достаточно велика. Не рекомендуется использовать коэффициент Спирмена, если имеет место неравномерное распределение значений измеряемой величины.
4. Как рассчитать коэффициент Спирмена?
Расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:
- Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию или убыванию.
- Определить разности рангов каждой пары сопоставляемых значений (d).
- Возвести в квадрат каждую разность и суммировать полученные результаты.
- Вычислить коэффициент корреляции рангов по формуле:
Определить статистическую значимость коэффициента при помощи t-критерия, рассчитанного по следующей формуле:
5. Как интерпретировать значение коэффициента Спирмена?
При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента меньше 0,3 — признаком слабой тесноты связи; значения более 0,3, но менее 0,7 — признаком умеренной тесноты связи, а значения 0,7 и более — признаком высокой тесноты связи.
Также для оценки тесноты связи может использоваться шкала Чеддока:
xy
Теснота (сила) корреляционной связи
менее 0.3
слабая
от 0.3 до 0.5
умеренная
от 0.5 до 0.7
заметная
от 0.7 до 0.9
высокая
более 0.9
весьма высокая
Статистическая значимость полученного коэффициента оценивается при помощи t-критерия Стьюдента. Если расчитанное значение t-критерия меньше табличного при заданном числе степеней свободы, статистическая значимость наблюдаемой взаимосвязи — отсутствует. Если больше, то корреляционная связь считается статистически значимой.
Суть корреляционного анализа
Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.
Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.
Оценка
Для оценки достоверности и эффективности модели связей необходимо построить матрицу коэффициентов. Коэффициент в случае парной корреляции вычисляется по формуле:
Диапазон значений коэффициента ограничивается показателями от -1 до +1. Если итоговое значение было получено со знаком плюс, то между рассматриваемыми переменными имеется прямая связь. Если в результате расчетов значение оказалось отрицательным, то связь будет обратной, то есть при увеличении одного из показателей другой связанный с ним фактор будет уменьшаться. Пример прямой связи – увеличение посевных площадей будет способствовать росту объема собираемой с полей продукции. Пример обратной связи – увеличение посевных площадей сопровождается снижением урожайности.
Качественный аспект тесноты связи между рассматриваемыми в аналитических расчетах показателями можно оценивать, основываясь на шкале Чеддока.
В соответствии с ее нормами связь будет расцениваться как сильная при значении коэффициента корреляции по абсолютным данным величины выше 0,7
Положительный или отрицательный знак сопровождает числовое значение – неважно, ориентироваться необходимо только на число. Если коэффициент после вычислений оказался ниже 0,3, то связь можно считать слабой
Для дальнейших этапов анализа выбираются факторы с высокой степенью связанности. Все остальные критерии, для которых установлена слабая связь, отбрасываются. На основании полученных сведений определяется вид математического уравнения регрессии. Рассчитывается численное значение оценки параметров регрессии, определяются качества полученной модели регрессии.
Корреляционный анализ
Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации).
Ограничения корреляционного анализа
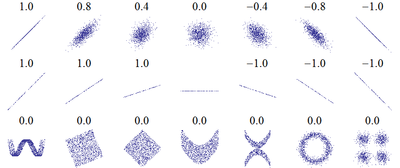
Множество корреляционных полей. Распределения значений (x,y){\displaystyle (x,y)} с соответствующими коэффициентами корреляций для каждого из них. Коэффициент корреляции отражает «зашумлённость» линейной зависимости (верхняя строка), но не описывает наклон линейной зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка). Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как дисперсия y равна нулю.
- Применение возможно при наличии достаточного количества наблюдений для изучения. На практике считается, что число наблюдений должно не менее чем в 5-6 раз превышать число факторов (также встречается рекомендация использовать пропорцию, не менее чем в 10 раз превышающую количество факторов). В случае если число наблюдений превышает количество факторов в десятки раз, в действие вступает закон больших чисел, который обеспечивает взаимопогашение случайных колебаний.
- Необходимо, чтобы совокупность значений всех факторных и результативного признаков подчинялась многомерному нормальному распределению. В случае если объём совокупности недостаточен для проведения формального тестирования на нормальность распределения, то закон распределения определяется визуально на основе корреляционного поля. Если в расположении точек на этом поле наблюдается линейная тенденция, то можно предположить, что совокупность исходных данных подчиняется нормальному закону распределения..
- Исходная совокупность значений должна быть качественно однородной.
- Сам по себе факт корреляционной зависимости не даёт основания утверждать, что одна из переменных предшествует или является причиной изменений, или то, что переменные вообще причинно связаны между собой, а не наблюдается действие третьего фактора.
Область применения
Данный метод обработки статистических данных весьма популярен в экономике, астрофизике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.


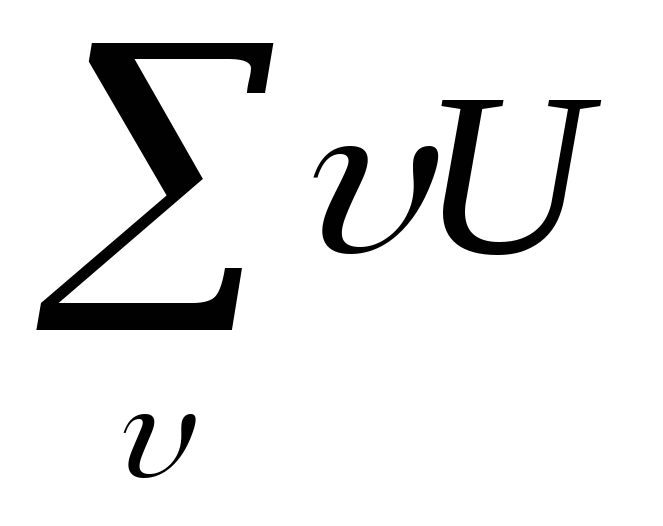 =
= ==169
==169