Сортировка методом пузырька в python

1.2 Выбор программного обеспечения по реализации ИТ

При написании программ для реализации сортировок массивов был использован язык программирования С++. Это один из широко используемых языков программирования, который можно использовать для написания программ, работающих в операционной среде Windows. Среда Borland C++ Builder 6- это сложный механизм, обеспечивающий высокоэффективную работу программиста

Интегрированная среда разработки C++ Builder представляет собой многооконную систему. Вид интегрированной среды разработки (интерфейс) может различаться в зависимости от настроек. Кроме стандартных окон, на экране могут присутствовать и другие окна, отображаемые при вызове соответствующих средств, например, Image Editor (Редактор изображений). Окна C++ Builder (но не главное) можно перемещать, убирать с экрана, а также изменять их размеры.

Несмотря на наличие многих окон, C++ Builder является одно-документной средой, т.е. позволяет одновременно работать только с одним приложением (проектом приложения). Название проекта приложения выводится в строке заголовка главного окна в верхней части экрана.

Если свернуть главное окно, то происходит минимизация всего интерфейса C++ Builder и, соответственно, всех открытых окон. При закрытии главного окна работа с C++ Builder прекращается.

Borland C++ Builder 6, вобрав в себя всё самое лучшее от предыдущих версий, предоставляет ряд новых возможностей. Так, например, стал более удобным и современным интерфейс среды программирования, создаваемые C++ Builder программы учитывают архитектуру современных процессоров, существенно расширены возможности отладчика.

Borland C++ Builder 6 может работать в среде операционных систем от Windows 95 до Windows XP. Особенных требований к компьютеру система не предъявляет, за исключением того, что процессор должен быть типа Pentium, оперативной памяти — не менее 32 Мбайт и достаточное количество свободной дисковой памяти.

Сортировка методом Пузырька. Реализация алгоритма на языке Python.

Довольно часто при решении задач приходится сортировать значения в списке (массиве) по возрастанию или убыванию. Существует большое количество различных алгоритмов сортировки. Они отличается друг от друга временем выполнения (вычислительной сложностью), используемой памятью, а также сложностью в понимании и реализации.

Можете просмотреть следующее видео — изображающее принцип работы некоторых алгоритмов сортировки:

Один из самый простых алгоритмов сортировки, изучаемый в школьном курсе информатики — «Сортировка методом Пузырька». Его нельзя назвать быстрым, но он очень прост в понимании и реализации. Подходит для сортировки небольших списков (массивов).

Работу данного алгоритма представил в виде танца коллектив из Финляндии

  Как видно из видео процесс сортировки заключается в следующем:

1. Сравнивается i-ый элемент списка с i+1 — ым. Если больший из них имеет меньший порядковый номер, то они меняются местами (для сортировки по возрастанию)
2. Таким образом, самый большой элемент  сдвигается в конец списка
3. Далее процесс повторяется, но не до конца списка, а до последнего отсортированного элемента

Например:

Дан список (массив): 0, 5, 8, 4, 9, 3

Расположим элементы списка в процессе убывания. Т.е. если элемент меньше своего соседа справа — меняется с ним местами.

После первого прохождения по списку первый нолик становится на последнее место

Как можно заметить количество сравнений уменьшилось на единицу, так как число 0 — минимальное заняло свое законное место при первой итерации и сравнивать с ним нет смысла.

Продолжаем:

Последний шаг:

В итоге получаем отсортированный список:

Для списка из шести элементов достаточно выполнить  пять «проходов» по списку, поочередно сравнивая соседние элементы.

Напишем программу сортировки методом Пузырька на Python 3.

#создаем список
li = 
#вычисляем длину списка
n = len(li)
#внешний цикл отсчитывает количество "проходов" по списку
for j in range(0,n-1):
    #вложенный цикл сравнивает i-ый c i+1 -ым элементом и при необходимости меняет их местами
    #количество сравнений каждый раз уменьшается на величину j
    for i in range(0,n-j-1):
        if li < li:
            li,li = li, li
    print(j+1, "- ый проход цикла - ",end=" ")
    print(li)
print(li)

Задачи:

1. Отсортировать список по возрастанию суммы цифр чисел
2. Дан список целых чисел, состоящий из 30 элементов. Найти сумму пяти самых больших и пяти самых маленьких элементов списка.

Опубликовано в рубрике Программирование Метки: Python, алгоритмы, массив, программирование, Сортировка, Список

Формат dat , вариант 2:

Название формата
Файл данных Minecraft

Оригинальное название
Minecraft Data File

Как открыть файл winmail dat?

Если приведенный выше метод не помогает, то то, что вы можете сделать, это открыть файл с помощью блокнота, так как вы знаете, что блокнот открывает любой тип файла. Конечно, вы можете использовать любой другой текстовый редактор . После открытия файла в блокноте вы можете увидеть текст или код блоков, которые не имеют смысла. Но большинство файлов содержит некоторую информацию, которая будет в виде обычного текста. Эти данные могут указывать на формат файла.

Это означает, что это может быть файл изображения. Если вы полностью не можете понять, какой тип файла он есть, вы можете просто попробовать открыть его с таким количеством программ, сколько сможете. И если вам повезет, вы можете найти подходящую программу, которая может открыть вашу.

Разработчик:
Mojang Specifications

Описание расширения

Файл данных, используемый популярной игрой — своеобразными конструктором мира Minecraft
. Может содержать различные виды данных, например об инвентаре игрока, его месте размещения, информацию о мире. Обычно сжат при помощи -сжатия.

Информация об игроке, уровне, времени дня хранится в файле с именем level.dat
.

Другие способы передачи информации

Все еще возникают проблемы с открытием. Следующий раздел основан на материалах, первоначально написанных Джеймсом Хардином, Университетом Южной Каролины и Тедом Анагнозоном, штат Калифорния, Лос-Анджелес. Дайте полное имя файла, включая расширение.
. Эти шаги также должны работать в других пакетах, которые принимают вход таким образом.

Вот три альтернативных способа выявления мошеннических наблюдений. Если это необходимо, их можно заменить отсутствующими, а затем переменную в целом можно преобразовать в числовое значение , набрав. Он также позволяет автоматически преобразовывать процентные данные. Люди могут непреднамеренно вводить пробелы в ячейки, которые в противном случае пустые.

Эти файлы могут также содержать «участки» уровня, которые загружаются по мере перемещения игрока по миру. Однако данный формат применялся преимущественно до версии 1.3 beta.

Более новый формат называется «Region», в нем участки уровня находятся в файла.MCR. Патчем 1.2.1 был введен формат «Anvil» и файлы с расширением.MCA.

DAT-файлы в Minecraft различались на протяжение всех выпусков игры. Поэтому файл.DAT из одной версии игры может быть несовместим с другой версией.

Обновлено: 17.09.2016г.

Алгоритмы сортировки на собеседовании

Алгоритмов сортировки достаточно много, и вряд ли можно встретить программиста, который может по памяти написать реализацию хотя бы половины из них.

На самом деле, программисты просто гуглят необходимую реализацию. Конечно, они имеют представление о принципах их работы, потому что в своё время рассмотрели несколько алгоритмов, как, например, сортировка пузырьком.

Кроме того, в Python и других языках программирования существуют встроенные функции, которые производят сортировку быстро и эффективно.

На собеседованиях спрашивают про алгоритмы сортировки, но это не значит, что от будущего работника требуют написать их реализацию или придумать свой. Работодатель требует от специалиста следующее:

• Уметь классифицировать алгоритмы сортировки.
• Знать преимущества и недостатки популярных алгоритмов, чтобы понимать, когда каждый из них лучше использовать.
• Понимать, что такое сложность алгоритма и как с её помощью определять, подходит ли он для решения данной задачи.

Использовать

Пузырьковая сортировка — алгоритм сортировки, который непрерывно просматривает список, меняя местами элементы, пока они не появятся в правильном порядке. Список был построен в декартовой системе координат, где каждая точка ( x , y ) указывает, что значение y хранится в индексе x . Затем список будет отсортирован пузырьковой сортировкой по значению каждого пикселя

Обратите внимание, что сначала сортируется самый большой конец, а меньшим элементам требуется больше времени, чтобы переместиться в правильное положение.

Хотя пузырьковая сортировка является одним из самых простых алгоритмов сортировки для понимания и реализации, ее сложность O ( n 2 ) означает, что ее эффективность резко снижается в списках, состоящих из более чем небольшого числа элементов. Даже среди простых алгоритмов сортировки O ( n 2 ) такие алгоритмы, как сортировка вставкой , обычно значительно более эффективны.

Из-за своей простоты пузырьковая сортировка часто используется для знакомства с концепцией алгоритма или алгоритма сортировки для начинающих студентов- информатиков . Тем не менее, некоторые исследователи, такие как Оуэн Астрахан , пошли на многое, чтобы осудить пузырьковую сортировку и ее неизменную популярность в образовании по информатике, рекомендуя даже не преподавать ее.

Жаргон Файл , который лихо звонков bogosort «архетипический извращенно ужасный алгоритм», также вызывает пузырьковую сортировку «общий плохой алгоритм». Дональд Кнут в своей книге «Искусство компьютерного программирования» пришел к выводу, что «пузырьковой сортировке, похоже, нечего рекомендовать, кроме броского названия и того факта, что она приводит к некоторым интересным теоретическим проблемам», некоторые из которых он затем обсуждает.

Пузырьковая сортировка асимптотически эквивалентна по времени работы сортировке вставкой в ​​худшем случае, но эти два алгоритма сильно различаются по количеству необходимых перестановок. Экспериментальные результаты, такие как результаты Astrachan, также показали, что сортировка вставкой работает значительно лучше даже в случайных списках. По этим причинам многие современные учебники алгоритмов избегают использования алгоритма пузырьковой сортировки в пользу сортировки вставкой.

Пузырьковая сортировка также плохо взаимодействует с современным оборудованием ЦП. Он производит как минимум вдвое больше записей, чем сортировка вставкой, вдвое больше промахов в кеш и асимптотически больше ошибочных прогнозов переходов . Эксперименты с сортировкой строк Astrachan в Java показывают, что пузырьковая сортировка примерно в пять раз быстрее сортировки вставкой и на 70% быстрее сортировки по выбору .

В компьютерной графике пузырьковая сортировка популярна благодаря своей способности обнаруживать очень маленькую ошибку (например, замену всего двух элементов) в почти отсортированных массивах и исправлять ее с линейной сложностью (2 n ). Например, он используется в алгоритме заполнения многоугольника, где ограничивающие линии сортируются по их координате x в определенной строке сканирования (линия, параллельная оси x ), а с увеличением y их порядок изменяется (два элемента меняются местами) только при пересечения двух линий. Пузырьковая сортировка — это стабильный алгоритм сортировки, как и сортировка вставкой.

Проточная порометрия

Перенос жидкости или газа через пористую
среду связан с параметрами этой среды.
Проточный метод изучения пористой
структуры основан на зависимости
удельной производительности от параметров
пористости. Расчет основан на уравнении
Пуазейля:

π r4∆P

V= ———— (4.25)

8ηδ

 Модель упрощена до представления
мембраны как пористого тела с прямыми
цилиндрическими порами. Реальность
поры, т.е. ее извилистость, шероховатость,
анизотропность, учитывается эмпирическими
коэффициентами.

Рис. 4.67. Ячейка для определения среднего
размера пор в мембранах:1-верхняя
крышка;

2-уплотнителъное кольцо;

3-мембрана;

4-пористая подложка;

5-сетка; 6-нижняя крышка;

7-корпус ячейки;

8-уплотнительная прокладка (резиновое
кольцо)

Для стандартизации условий испытаний
используют ячейки с постоянной площадью
мембраны (рис.4.67).
На дно нижней крышки 6 помещают
металлическую сетку 5, затем подложку
4, испытываемую мембрану 3, уплотнительное
кольцо 2. Толщину мембраны предварительно
измеряют микрометром. Регулируют
давление сжатого воздуха и измеряют
производительность образца по жидкости,
заливаемой в ячейку.

Если бы поры в мембране были все одинаковы,
мы имели бы графическую зависимость
проницаемости от давления как на левой
части рис.4.68.
Сначала мембрана остается непроницаемой,
поскольку для продавливания жидкости
через любую пору необходимо некоторое
давление. ВеличинаР_minопределяется смачиваемостью мембраны
жидкостью и размером самых больших пор.

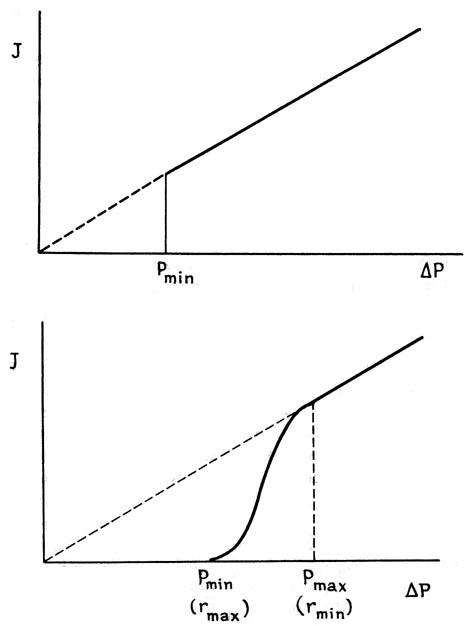
Рис. 4.68. Зависимость удельной
производительности мембраны от
приложенного давления для идеальной
(слева) и реальной (справа) мембраны

В реальной мембране всегда существует
некоторое распределение пор по размерам,
поэтому кривая проницаемости сначала
имеет S-образный участок, а затем линейный.
Уравнение Пуазейля можно записать для
выражения количества жидкости, прошедшей
через мембрану площадью S с числом пор
N на единице площади за время t:

π r4∆PtSN

V= ————— (4.26)

8ηδ

В свою очередь N= П/ πr3,
где П — общая пористость мембраны, отсюда

8 ηδV8 ηG

r= ————— = ———— (4.27)

П∆PtSП∆P

Расчет, проведенный по данным линейного
участка зависимости на рис.4.68,
даст величину среднего размера пор
мембраны, что для мембран с узким
распределением пор является достаточной
характеристикой.

Принимаемые в методе допущения (о
цилиндричности и неизвилистости пор,
постоянстве сечения по всей длине
отдельных пор, равенстве общей и
эффективной, т.е. участвующей в транспорте
жидкости, пористости мембраны) вносят
определенные погрешности в оценку
среднего размера пор ультрафильтрационных
мембран. В частности, извилистость
реальных пор приводит при расчетах к
заниженным значениям их размеров. К
заниженным результатам приводит и
различие в общей и эффективной пористости
мембран вследствие ориентационной
упорядоченности пор.

К уменьшению величины эффективной
пористости по сравнению со значениями,
используемыми в расчетах, а, следовательно,
и занижению результатов, приводит
наличие в мембранах не участвующих в
течении пристенных слоев связанной
воды.

Толщина таких гидродинамически
неподвижных слоев составляет примерно
1 нм и, следовательно, вклад этого фактора
становится весьма ощутимым для
сравнительно тонкопористых мембран.С
другой стороны, асимметрия структуры
мембраны приводит к завышенным значениям
средних размеров пор. Это в определенной
мере нивелирует их занижение вследствие
неучета пристенных слоев воды, извилистости
и ориентационной упорядоченности пор.

Итак, в реальной мембране существуют
поры разного размера, поэтому зависимость
Gот ΔР на рисунке 4.67 имеетS-образный характер, т.е.
по мере повышения давления в работу
включаются все меньшие поры. Если
проводить ступенчатое по ΔР исследование,
то на каждый прирост ΔР наложится
прирост вG(рисунок 4.69).

Рис. 4.69. Графическая дифференциация
зависимости удельной производительности
мембраны от приложенного давления

В расчете будем использовать
модифицированные уравнения Пуазейля
и Лапласа:

π∙r4_i—jt∙S∙N_i—j

V_i—j= ────────── ∙P_j(4.28)

8 ηδ

P_j=
2σ/r_i—j(4.29)

Из них получим расчетные выражения для
rиN:

r∙δ

N_i—j= ──── ∙P3_j∙ΔG_i—j(4.30)

2πσ4

r_i—j= 2σ/P_j(4.31)

Рассчитав для каждого интервала i-jэти две величины, получим информацию
для построения зависимостиN_i—jдля каждого интервалаr_i—j(рис. 4.70).

Рис. 4.70. Зависимость «количество пор
– радиус пор»,

т.е. кривая распределения пор по размеру

Распределение пор по размеру является
наиболее объективной характеристикой
пористой мембраны.

2.1 Сортировка массива простыми включениями

Метод простых вставок предполагает разделение всего массива элементов на упорядоченную часть, которая вначале содержит лишь один элемент, и неупорядоченную. Очередной элемент из неупорядоченной части вставляется в определенное место упорядоченной части, проходя сравнение с ее элементами. При поиске подходящего места удобно чередовать сравнения и пересылки, т.е. как бы «просеивать» выбранный элемент, сравнивая его с очередным элементом a и либо вставляя, либо пересылая a направо и продвигаясь налево. Заметим, что «просеивание» может закончиться при двух различных условиях: найден элемент a с ключом меньшим, чем ключ x или достигнут левый конец готовой последовательности.

При этом упорядоченная часть удлиняется на один элемент. Сортировка заканчивается при окончании неупорядоченной части.

При данной сортировке общее число сравнений приблизительно равно

,

При этом требуется количество проходов по данным P

Рисунок 5. Пример сортировки массива простыми включениями

Число Ci сравнений ключей при i-м просеивании составляет самое большее i-1, самое меньшее 1 и, если предположить, что все перестановки n ключей равновероятны, в среднем равно i/2. Число Мi пересылок (присваиваний) равно Ci+2 (учитывая барьер). Поэтому общее число сравнений и пересылок есть

Cmin = n-1 Mmin = 2 (n-1)

Cср. = (n2+n-2) /4 Mср. = (n2+9n-10) /4

Cmax = ( (n2+n) — 1) /2 Mmax = (n2+3n-4) /2.

Алгоритм сортировки простыми включениями можно легко улучшить, пользуясь тем, что готовая последовательность a ,…, a , в которую нужно включить новый элемент, уже упорядочена. Поэтому место включения можно найти значительно быстрее, применив бинарный поиск, который исследует средний элемент готовой последовательности и продолжает деление пополам, пока не будет найдено место включения.

Анализ

Пример пузырьковой сортировки. Начиная с начала списка, сравните каждую соседнюю пару, поменяйте их местами, если они не в правильном порядке (последняя меньше первой). После каждой итерации нужно сравнивать на один элемент меньше (последний), пока не останется больше элементов для сравнения.

Производительность

Пузырьковая сортировка имеет наихудший случай и среднюю сложность О ( n 2 ), где n — количество сортируемых элементов. Большинство практических алгоритмов сортировки имеют существенно лучшую сложность в худшем случае или в среднем, часто O ( n  log  n ). Даже другое О ( п 2 ) алгоритмы сортировки, такие как вставки рода , как правило , не работать быстрее , чем пузырьковой сортировки, а не более сложным. Следовательно, пузырьковая сортировка не является практическим алгоритмом сортировки.

Единственное существенное преимущество пузырьковой сортировки перед большинством других алгоритмов, даже быстрой сортировкой , но не сортировкой вставкой , заключается в том, что в алгоритм встроена способность определять, что список сортируется эффективно. Когда список уже отсортирован (в лучшем случае), сложность пузырьковой сортировки составляет всего O ( n ). Напротив, большинство других алгоритмов, даже с лучшей средней сложностью , выполняют весь свой процесс сортировки на множестве и, следовательно, являются более сложными. Однако сортировка вставкой не только разделяет это преимущество, но также лучше работает со списком, который существенно отсортирован (с небольшим количеством инверсий ).

В случае больших коллекций следует избегать пузырьковой сортировки. Это не будет эффективно в случае коллекции с обратным порядком.

Кролики и черепахи

Расстояние и направление, в котором элементы должны перемещаться во время сортировки, определяют производительность пузырьковой сортировки, поскольку элементы перемещаются в разных направлениях с разной скоростью. Элемент, который должен переместиться в конец списка, может перемещаться быстро, потому что он может принимать участие в последовательных заменах. Например, самый большой элемент в списке будет выигрывать при каждом обмене, поэтому он перемещается в свою отсортированную позицию на первом проходе, даже если он начинается с начала. С другой стороны, элемент, который должен двигаться к началу списка, не может перемещаться быстрее, чем один шаг за проход, поэтому элементы перемещаются к началу очень медленно. Если наименьший элемент находится в конце списка, потребуется n -1 проход, чтобы переместить его в начало. Это привело к тому, что эти типы элементов были названы кроликами и черепахами соответственно в честь персонажей басни Эзопа о Черепахе и Зайце .

Были предприняты различные усилия по устранению черепах, чтобы повысить скорость сортировки пузырей. Сортировка коктейлей — это двунаправленная сортировка пузырьков, которая идет от начала до конца, а затем меняет свое направление, идя от конца к началу. Он может довольно хорошо перемещать черепах, но сохраняет сложность наихудшего случая O (n 2 ) . Комбинированная сортировка сравнивает элементы, разделенные большими промежутками, и может очень быстро перемещать черепах, прежде чем переходить к все меньшим и меньшим промежуткам для сглаживания списка. Его средняя скорость сопоставима с более быстрыми алгоритмами вроде быстрой сортировки .

Пошаговый пример

Возьмите массив чисел «5 1 4 2 8» и отсортируйте его от наименьшего числа к наибольшему с помощью пузырьковой сортировки. На каждом этапе сравниваются элементы, выделенные жирным шрифтом . Потребуется три прохода;

Первый проход

( 5 1 4 2 8) → ( 1 5 4 2 8). Здесь алгоритм сравнивает первые два элемента и меняет местами, поскольку 5> 1.

(1 5 4 2 8) → (1 4 5 2 8), поменять местами, поскольку 5> 4

(1 4 5 2 8) → (1 4 2 5 8), поменять местами, поскольку 5> 2

(1 4 2 5 8 ) → (1 4 2 5 8 ). Теперь, поскольку эти элементы уже в порядке (8> 5), алгоритм не меняет их местами.

Второй проход

( 1 4 2 5 8) → ( 1 4 2 5 8)

(1 4 2 5 8) → (1 2 4 5 8), поменять местами, поскольку 4> 2

(1 2 4 5 8) → (1 2 4 5 8)

(1 2 4 5 8 ) → (1 2 4 5 8 )

Теперь массив уже отсортирован, но алгоритм не знает, завершился ли он. Алгоритм нужен один весь проход без какой — либо свопа знать сортируется.

Третий проход

( 1 2 4 5 8) → ( 1 2 4 5 8)

(1 2 4 5 8) → (1 2 4 5 8)

(1 2 4 5 8) → (1 2 4 5 8)

(1 2 4 5 8 ) → (1 2 4 5 8 )

2.4 Пирамидальная сортировка

Пирамида определяется как последовательность ключей

hl, hl+1,…, hr, такая, что hi <= h2i, hi <= h2i+1

для всякого i =l,…,r/2. Если двоичное дерево представлено в виде массива, как показано на рис.1, то, следовательно, деревья сортировки на рис.2 и 3 являются пирамидами, и, в частности, элемент h1 пирамиды является ее наименьшим элементом h1 = min (h1… hn).

Теперь предположим, что дана пирамида с элементами hl+1,…, hr для некоторых значений l и r и нужно добавить новый элемент x для того, чтобы сформировать расширенную пирамиду hl,…, hr. Возьмем, например, исходную пирамиду h1,…,h7, показанную на рис.2, и расширим эту пирамиду «влево», добавив элемент h1=44. Новый элемент x сначала помещается в вершину дерева, а затем «просеивается» по пути, на котором находятся меньшие по сравнению с ним элементы, которые одновременно поднимаются вверх; таким образом формируется новая пирамида. На рисунке 8 продемонстрирована пирамидальная сортировка.

Рисунок 8. Процесс построения дерева

В данном примере значение 44 сначала меняется местами с 06, затем 12, и так формируется дерево. Далее процесс просеивания будем формулировать следующим образом: i, j — пара индексов, обозначающих элементы, которые нужно менять местами на каждом шаге просеивания.

Для восьми элементов из нашего примера минимальное и максимальное количества пересылок дают следующие исходные последовательности:

Мmin = 13 для последовательности

94, 67, 44, 55, 12, 42, 18, 6

Mmax=24 для последовательности

18, 42, 12, 44, 6, 55, 67, 94

Среднее число пересылок равно приблизительно nlog (n) /2 и отклонения от этого значения сравнительно малы.

Метод пузырьковой сортировки в Паскале

Замечание 1

Под сортировкой на языке Паскаль понимается упорядочение массива данных (как правило по возрастанию или по убыванию). Сортировка названа пузырьковой из-за аналогии с погруженными в воду вертикальным массивом. Массив — это вода, а его самые маленькие элементы являются пузырьками, которые стремятся всплыть вверх.

Алгоритм может быть представлен следующим образом:

1. Для выполнения процесса сортировки применяются два цикла, причём один цикл вложен в другой. Первый цикл применяется для формирования шагов, второй — под-шагов.

2. Основой алгоритма является сравнение двух элементов. К примеру, есть массив с десятью элементами. Элементы подлежат сравнению парами: 1 и 2, 2 и 3, 3 и 4 ,4 и 5 ,6 и 7 и так далее. Если при выполнении сравнения текущий элемент больше по величине чем следующий, то они меняются местами. К примеру, если первый элемент пять, а второй два, то они меняются местами.

3. Процесс сортировки пузырьковым методом подразделяется на шаги. Каждый шаг предполагает сравнение пары элементов. Итогом работы каждого шага является выстраивание самого большого элемента в конец массива. Таким образом после первого шага наибольший элемент массива окажется на последнем месте. При втором шаге действия выполняются по отношению ко всем элементам, исключая последний. Далее снова ищется наибольший элемент, и он перемещается опять в окончание массива, который в данный момент обрабатывается. И так процесс повторяется до полного окончания сортировки.

Приведём наглядный пример. Имеется массив, включающий в себя семь элементов: 2, 5, 11, 1, 7, 8, 3. Процесс сортировки изображён на рисунке 1.

Рисунок 1. Процесс сортировки. Автор24 — интернет-биржа студенческих работ

Далее сформируем собственно программу, реализующую данный алгоритм на языке Паскаль. Ниже приведён текст программы:

Замечание 2

Следует подчеркнуть, что элемент k нужен только для того, чтобы выполнить обмен местами двух элементов. Это объясняется тем, что Паскаль не имеет команды, которая смогла бы осуществить эту операцию. Это вынуждает формировать данную процедуру программным путём, вводя добавочный элемент для обмена.

2.8 Теоретическое сравнение сортировок методом простых вставок и методом пузырька

Выполним по рекомендованной литературе теоретическое сравнение алгоритмов сортировок, рассматриваемых в данном курсовом проекте. Основным критерием сравнения сортировок является их эффективность, то есть число сравнений и число пересылок. Данные показатели также влияют на время сортировки. Укажем основные формулы, использующиеся для вычисления эффективности данных сортировок:

− число сравнений ключей элементов при i-ом просеивании;

−минимальное число сравнений ключей;

− максимальное число сравнений ключей;

− среднее число сравнений ключей;

− число пересылок (присваиваний) элементов при i-ом просеивании;

− минимальное число пересылок

− максимальное число пересылок

− среднее число пересылок

− размер массива;

Рассмотрим сортировку методом простых вставок

Рассмотрим сортировку методом пузырька

На основе данных методических формул составим сравнительную таблицу для сортировок методом простых вставок и методом пузырька:

Таблица 2. Сравнительный анализ сортировок методом простых вставок и методом пузырька

Размер массива	Метод простых вставок	Метод пузырька
Число сравнений ключей (среднее значение)	Число пересылок (среднее значение)	Число сравнений ключей (среднее значение)	Число пересылок (среднее значение)
32	263	329	256	384
64	1039	1163	1024	1536
128	4127	4379	4096	6144
256	16447	16953	16384	24576
512	65663	131835	65536	98304
1024	262399	264443	262144	393216

На основе полученных в таблице 2 значений составим сравнительные графики, для числа сравнений ключей и для числа пересылок по обоим методам сортировки:

Рисунок 10. Графики числа сравнений ключей: число сравнений ключей П — для метода пузырька, число сравнений ключей В — для метода простых вставок.

На основе полученных графиков можно сказать, что число сравнений ключей в сортировке методом пузырька число сравнений больше, чем в сортировке методом вставок. Следовательно по данному критерию эффективность сортировки методом простых вставок выше, чем методом пузырька.

Рисунок 11. Графики числа пересылок в сортировках: число пересылок П — для метода пузырька, число пересылок В — для метода простых вставок.

Основываясь на полученных графиках можно сказать, что при малых значениях размерности массива число пересылок для обоих методов примерно одинаково. При относительно больших размерах массива (от 512 и более) число пересылок в методе

пузырька возрастает быстрее, чем в методе простых вставок. Следовательно, эффективность метода вставок выше по данной характеристике.

Ссылаясь на таблицу 1 можно также отметить, что сортировка методом пузырька требует больше времени, чем сортировка методом вставок.

Из чего следует, что в целом сортировка методом простых вставок эффективнее сортировки методом пузырька.

Как создать пузырьковую сортировку

Вот что нам придется делать для создания пузырьковой сортировки:

• Создать два цикла , чтобы проходить по всем элементам массива раз ( это размер массива).
• Сравнивать ячейки массива, с помощью оператора ветвления .
• Менять местами значения ячеек.

В примере ниже мы предложили пользователю заполнить массив, который мы дальше отсортируем используя пузырьковую сортировку.

#include <iostream>

using namespace std;

int main() {
setlocale(LC_ALL, «rus»);

int digitals; // объявили массив на 10 ячеек

cout << «Введите 10 чисел для заполнения массива: » << endl;

for (int i = 0; i < 10; i++) {
cin >> digitals; // «читаем» элементы в массив
}

for (int i = 0; i < 10; i++) {
for (int j = 0; j < 9; j++) {
if (digitals > digitals) {
int b = digitals; // создали дополнительную переменную
digitals = digitals; // меняем местами
digitals = b; // значения элементов
}
}
}

cout << «Массив в отсортированном виде: «;

for (int i = 0; i < 10; i++) {
cout << digitals << » «; // выводим элементы массива
}
system(«pause»);
return 0;
}

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

#include <iostream>   usingnamespacestd; intmain(){ setlocale(LC_ALL,»rus»); intdigitals10;// объявили массив на 10 ячеек cout<<«Введите 10 чисел для заполнения массива: «<<endl; for(inti=;i<10;i++){ cin>>digitalsi;// «читаем» элементы в массив } for(inti=;i<10;i++){ for(intj=;j<9;j++){ if(digitalsj>digitalsj+1){ intb=digitalsj;// создали дополнительную переменную digitalsj=digitalsj+1;// меняем местами digitalsj+1=b;// значения элементов } } } cout<<«Массив в отсортированном виде: «; for(inti=;i<10;i++){ cout<<digitalsi<<» «;// выводим элементы массива } system(«pause»); return; }

Давайте поподробнее разберем строки 16 — 24 (здесь находится пузырьковая сортировка)

1. В строке 16: мы создали первый цикл .
2. В строке 17: аналогично был создан второй, но уже вложенный цикл.
3. В строке 18: происходит сравнивание двух элементов.
   • Если  результат этого условия положительный, то мы меняем значение элементов.
   • Если же результат отрицателен, то мы пропускаем этап смены значений.
4. В строке 19: создали переменную , чтобы менять значения ячеек и местами.

Давайте посмотрим, что выведет программа выше при запуске:

sort_puzerek.cpp

Введите 10 чисел для заполнения массива:
5 3 6 2 7 0 2 8 9 10

Массив в отсортированном виде: 0 2 2 3 5 6 7 8 9 10
Process returned 0 (0x0) execution time : 0.005 s
Press any key to continue.

2.3 Сортировка массива сложным выбором (с помощью двоичного дерева)

Метод сортировки основан на повторном выборе наименьшего ключа среди n элементов, затем среди n-1 элементов и т.д. Понятно, что поиск наименьшего ключа из n элементов требует n-1 сравнений, а поиск его среди n-1 элементов n-2 сравнений. Улучшить сортировку выбором можно в том случае, если получать от каждого прохода больше информации, чем просто указание на один, наименьший элемент. Например, с помощью n/2 сравнений можно определить наименьший ключ из каждой пары, при помощи следующих n/4 сравнений можно выбрать наименьший из каждой пары таких наименьших ключей и т.д. Наконец при помощи всего n-1 сравнений мы можем построить дерево, как показано на рис.1, выбора и определит корень, как наименьший ключ. На втором шаге мы спускаемся по пути, указанном наименьшим ключом, и исключаем его, последовательно заменяя либо на «дыру» (или ключ бесконечность), либо на элемент, находящийся на противоположной ветви промежуточного узла Элемент оказывается в корне дерева, вновь имеет наименьший ключ среди оставшихся и может быть исключен. После n таких шагов дерево становится пустым (т.е. состоит из «дыр»), и процесс сортировки закончен.

При сортировке с помощью дерева задача хранения информации стала сложнее и поэтому увеличилась сложность отдельных шагов; в конечном счете, для хранения возросшего объема информации нужно строить некую древовидную структуру. Также желательно избавиться от необходимости в дырах, которые в конце заполняют дерево и приводят к большому числу ненужных сравнений. Механизм сортировки методом бинарного дерева отображен на рисунке 7.

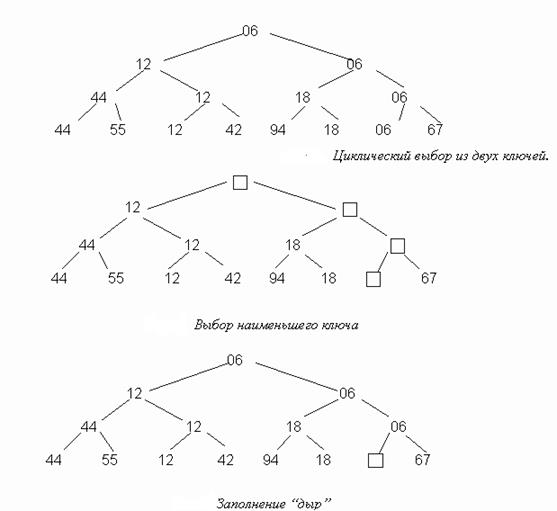
Рисунок 7. Сортировка бинарным деревом

Сложность[править]

В данной сортировке выполняются всего два различных вида операции: сравнение элементов и их обмен. Поэтому время всего алгоритма , где — время, затрачиваемое на сравнение элементов, а — время, за которое мы производим все необходимые обмены элементов.

Так как в алгоритме меняться местами могут только соседние элементы, то каждый обмен уменьшает количество инверсий на единицу. Следовательно, количество обменов равно количеству инверсий в исходном массиве вне зависимости от реализации сортировки. Максимальное количество инверсий содержится в массиве, элементы которого отсортированы по убыванию. Несложно посчитать, что количество инверсий в таком массиве . Получаем, что .

В неоптимизированной реализации на каждой итерации внутреннего цикла производятся сравнений, а так как внутренний цикл запускается также раз, то за весь алгоритм сортировки производятся сравнений.

В оптимизированной версии точное количество сравнений зависит от исходного массива. Известно, что худший случай равен , а лучший — . Следовательно, .

В итоге получаем .

Таблица 2: Сортировка пузырьком в многопоточном режиме

1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	2	3	4	5	6	7	8	9	10	11	12	13	14
2	1	3	4	5	6	7	8	9	10	11	12	13	14
2	3	1	4	5	6	7	8	9	10	11	12	13	14
3	2	4	1	5	6	7	8	9	10	11	12	13	14
3	4	2	5	1	6	7	8	9	10	11	12	13	14
4	3	5	2	6	1	7	8	9	10	11	12	13	14
4	5	3	6	2	7	1	8	9	10	11	12	13	14
5	4	6	3	7	2	8	1	9	10	11	12	13	14
5	6	4	7	3	8	2	9	1	10	11	12	13	14
6	5	7	4	8	3	9	2	10	1	11	12	13	14
6	7	5	8	4	9	3	10	2	11	1	12	13	14
7	6	8	5	9	4	10	3	11	2	12	1	13	14
7	8	6	9	5	10	4	11	3	12	2	13	1	14
8	7	9	6	10	5	11	4	12	3	13	2	14	1
8	9	7	10	6	11	5	12	4	13	3	14	2	1
9	8	10	7	11	6	12	5	13	4	14	3	2	1
9	10	8	11	7	12	6	13	5	14	4	3	2	1
10	9	11	8	12	7	13	6	14	5	4	3	2	1
10	11	9	12	8	13	7	14	6	5	4	3	2	1
11	10	12	9	13	8	14	7	6	5	4	3	2	1
11	12	10	13	9	14	8	7	6	5	4	3	2	1
12	11	13	10	14	9	8	7	6	5	4	3	2	1
12	13	11	14	10	9	8	7	6	5	4	3	2	1
13	12	14	11	10	9	8	7	6	5	4	3	2	1
13	14	12	11	10	9	8	7	6	5	4	3	2	1
14	13	12	11	10	9	8	7	6	5	4	3	2	1
14	13	12	11	10	9	8	7	6	5	4	3	2	1