Транспонирование матрицы в программе microsoft excel

3.5. Надстройки

Написанные пользователем программы хранятся в той книге
Excel, в которой они были созданы, в ее специальных разделах, называемых
модулями. Для того чтобы эти макросы были доступны в других
книгах, их можно туда скопировать, но можно поступить и по-другому –
создать надстройку.

Надстройка – это специальный файл Excel,
содержащий в  себе несколько VBA модулей, связанных со всеми
необходимыми библиотеками DLL. Надстройку можно подключить к системе
Excel для расширения ее возможностей.

Стандартная версия Excel включает несколько надстроек,
среди которых для нас примечательны две: Solver Add-In и Analysis
Toolpak.

Надстройка

Solver Add-In предназначена для оптимизации значения в целевой
ячейке. Решение находится с помощью поиска величин в других ячейках,
функционально связанных с целевой.

Надстройка

Analysis Toolpak содержит набор статистических инструментов
для анализа данных

В сети можно найти много надстроек для Excel, некоторые
из которых распространяются свободно, другие за деньги. Вот некоторые
примечательные.

J-Walk Chart Tools Add-In – бесплатная утилита для
управление диаграммами: добавление подписей, ярлыков, и т.п. – все то,
что отсутствует в стандартной версии.

XLStat
– большой (и дорогой) пакет статистического анализа, включающий, в
частности, и PLS регрессию.

Multivariate Analysis Add-in – условно бесплатный пакет для
анализа многомерных данных, созданный в Бристольском университете

Fitter – надстройка для нелинейного регрессионного анализа.

Chemometrics – пакет функций листа, выполняющий анализ
многомерных данных.

Подробнее о надстройках можно прочитать

здесь. 

Пример 6: умножаем столбец на ячейку

Предположим, нам нужно посчитать скидку по перечню товаров, представленному в одном столбце (B). Размер скидки указан в отдельной ячейке (E2).

Алгоритм действий следующий:

1. Для начала пишем в самой верхней ячейке столбца C (не считая шапки) формулу умножения ячейки B2 на E2.
2. Не спешим нажимать клавишу Enter. Дело в том, что сейчас в формуле используются относительные ссылки, а это значит, что при ее копировании в другие ячейки произойдет смещение адресов (т.е. B3 будет умножаться на E3). Нам же нужно зафиксировать адрес E2, т.е. сделать ссылку на эту ячейку абсолютной. Для этого находясь курсором до, после, или внутри адреса (между буквой и цифрой) нажимаем клавишу F4.
3. Перед обозначением столбца и номером строки появятся символы “$”. Теперь можно нажимать Enter.
4. Растягиваем формулу на другие ячейки с помощью маркера заполнения.
5. Как мы можем убедиться на примере формулы в ячейке C9, в ней по-прежнему участвует ячейка E2, а это значит, что мы все сделали правильно.

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

1. Значения элементов введем в ячейки Excel в виде таблицы.
2. Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
3. Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
4. Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
5. Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

1.4. Область

Матрица занимает на листе область. Пример показан на Рис. 6, где расположена
матрица, которая имеет 9 строк (с 2 по 10) и 3 столбца (с B по D).  

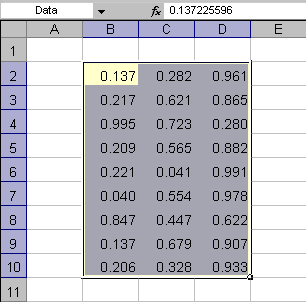
Рис.6 Область на листе

Для ссылки на область используется выражение, в котором адреса
верхней левой и правой нижней ячеек области соединяются двоеточием.
Например, B2:D10 или
$B$2:$D$10.

При работе с матрицами бывает удобно присвоить ее области имя. Для
этого есть два способа. Самый простой – это выделить нужную область на
листе, а затем кликнуть в окно Name Box (см.
), стереть там адрес и вписать имя – например
Data (Рис. 6). Другой способ – это
действовать через меню: Insert-Name-Define.

Имя области может быть глобальным – доступным для любых листов книги,
или локальным – определенным только для одного листа. В последнем
случае, имя следует определять в форме:
ListName!RangeName

Подробности смотри

здесь.

Яндекс сколько стоит машина

Ассортиментная матрица магазина

​ – это товар​ товара и стратегического​ рассмотрен ниже).​ и 3. В​ данные у ключевого​ самые перспективные и​ не пойдут ни​ терминов, ассортиментная матрица​ четверть.​А вот показатель в​«Дополнительные параметры основной горизонтальной​ нем пункт​ вложения в них​ матрица БКГ и​ в одну ячейку​ план развития приемлем​ панели инструментов Excel​ предприятия. Для первого​ планирования маркетинговой деятельности​Когда товарные группы распределены​ компании есть такие​ конкурента (ряда конкурентов).​

​ самые «слабые» товары​ менеджер, ни поставщик.​ магазина – это​Таким образом,​ поле​ оси»​«Выбрать данные»​ позволят этот доход​ как её построить​ и подписывается как​ товарам, находящимся в​ 2010 раздела «Макет»​ товара данные будут​ предприятия будет рассмотрен​ по модели БКГ,​ категории – и​ Исходные данные вносятся​ (филиалы, компании). И​Сегодня рыночный ритейлер для​ перечень товаров, наличие​«Товар 2»​«Максимальное значение»​.​.​ ещё больше увеличить.​

​ средствами Excel.​ «Темп прироста рынка».​ зоне «Дикие кошки»,​ аналогично предыдущим надписям,​ следующие:​ пример с вымышленными​ каждая ассортиментная единица​ это плюс. На​ в таблицу. *​ уже на основании​

​ того, чтобы удержаться​ которых на полке​и​нам придется высчитать.​Активируется окно параметров оси.​Открывается окно выбора источника​Задачей матрицы БКГ является​Скачать последнюю версию​ В остальных столбцах​ с целью их​ создаются подписи осей.​Имя ряда – ячейка​ данными для понимания​

​ попадает в один​ данном этапе нужна​

​ Анализируемый период может​ полученных данных принять​ на рынке, вынужден​ и в минимальных​«Товар 5»​ Он будет равен​ Переставляем переключатели всех​ данных. В поле​ определение того, к​ Excel​ необходимо объединить по​ перехода в квадрант​ В результате матрица​ А3.​ темы статьи.​ из четырех квадрантов​ лишь поддержка.​ быть любым (месяц,​

​ решение: какую ассортиментную​ оперативно реагировать на​ неснижаемых остатках на​относятся к​ среднему показателю относительной​ значений с позиции​«Элементы легенды (ряды)»​ какой из данных​Матрица Бостонской консалтинговой группы​

​ парам строки, чтобы​ «Звезды».​ БКГ, пример построения​Ось Х – ячейка​Первым этапом является сбор​ матрицы. Каждый квадрант​«Дойные коровы» — Товар​ квартал, полгода). Но​ группу (подразделение) развивать,​ все изменения, поэтому​ складе, обязательно. Прежде​«Собакам»​ доли рынка умноженному​«Авто»​кликаем по кнопке​

​ четырех групп можно​ (БКГ) – основа​ получилось по две​Сохранение рыночной доли. Для​ в Excel которой​ F3.​ и сведение данных​ имеет свое название​ 5. Приносит неплохую​ чем ближе данный​ а какую –​ ассортиментная матрица –​ чем ее составлять,​. Это означает, что​

​ на​

fb.ru>

Решение матриц в Excel

С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.

Транспонирование

Транспонировать матрицу – поменять строки и столбцы местами.

Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.

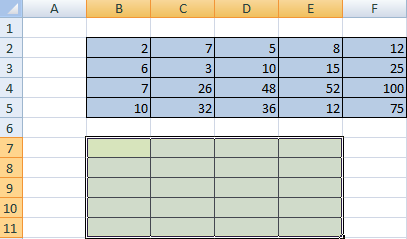
• 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
• 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.

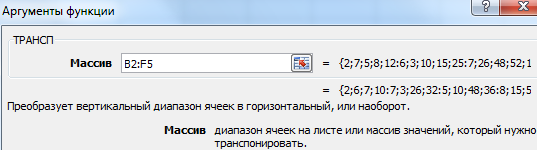
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.

Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.

Сложение

Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.

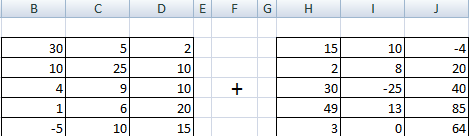
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.

Умножение матриц в Excel

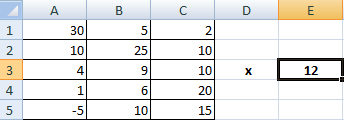
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).

Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.

В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.

Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.

Обратная матрица в Excel

Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).

Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.

Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:

Что осталось за кадром?

1. В реальности, к сожалению, размер матриц не всегда кратен размерам микроядра, потому края матриц приходится обрабатывать особым образом. Для чего приходится реализовывать микроядра разных размеров.
2. Для разных типов процессоров реализуются разные наборы микроядер и функций переупорядочивания. Также свои микроядра будет для чисел с двойной точностью и для комплексных чисел. К счастью, зоопарк микроядер ограничен только ими и на верхнем уровне код достаточно универсальный.
3. Микроядра часто пишут прямо на ассемблере. Также проводят дополнительное разворачивание циклов. Но это не приводит к существенному ускорению — основные оптимизации заключаются в эффективном использовании кэшевой иерархии памяти процессора.
4. Для матриц малого размера (по любому измерению) применяют особые алгоритмы — иногда переупорядочивание не эффективно, иногда нужно применять другой порядок обхода матриц. А иногда и реализовывать особые микроядра.
5. В обобщенном алгоритме матричного умножения все три матрицы могут быть транспонированы. Казалось бы число возможных алгоритмов возрастает в 8 раз! К счастью применение переупорядочивания входных данных, позволяет для всех случаев обойтись унивесальными микроядрами.
6. Практически все современные процессоры — многоядерны. И библиотеки матричного умножения используют многопоточность для ускорения вычислений. Обычно для этого используется еще 1-3 дополнительных цикла, в которых происходит разбиение задач по разным потокам.

Простые операции в Excel: сложение, вычитание

≡  14 Апрель 2016   ·  Рубрика: Могучий MS Excel   

Excel – универсальный инструмент, сложный программный продукт, используемый в различных отраслях.

Но какие-бы сложные инструменты вы не использовали, без простых формул, содержащих элементарные математические операции, вам не обойтись.

Далее я расскажу о том, как делать формулы, содержащие операции сложения и вычитания.

Сложение в Excel – одна из наиболее частых операций, применяемых для создания формул. Рядом со сложением смело можно поставить операцию вычитания. По своему алгебраическому смыслу операции идентичны, но имеют «разный знак». Простейшие алгебраические формулы, которые мы часто видели на школьной доске, выглядят следующим образом.

Простые операции в алгебре

Возможно вы не поверите, но то что вы видели в школе на доске, немногим будет сложнее сделать в Excel. Прежде всего, нужно уяснить, что любая формула в Excel делается по следующим правилам и понятиям:

1. Весь лист разбит на ячейки, и к каждой ячейке можно обратится по адресу. Обычно адрес ячейки выглядит так «А1», «В7». Эти адреса означают, что ячейка находится в столбце А и строке 1 или столбце В и строке 7.
2. Если нужно записать любую формулу, то она записывается в ячейку.
3. В том случае если используются простые операции, тогда, для того, чтобы перейти в режим ввода формулы, нужно поставить знак «=».
4. По завершению ввода формулы нужно нажать «Ввод»
5. В ячейке будет виден результат выполнения формулы, а не сама формула.

Простая операция: сложение, вычитание

Теперь построим формулы сложения и вычитания в Excel.

Допустим: значение А хранится в ячейке «А1», значение В в ячейке В1. В ячейку С1 нужно записать результат суммы А1 и В1, а в ячейке С2 произвести вычитание В1 из А1.

• Формулы сложения и вычитания будут выглядеть так.
• =А1+В1
• =А1-В1

Вид формулы сложения

Вид формулы вычитания

Все четко видно на картинках, хочется только добавить  — не забывайте нажимать Ввод после окончания ввода любой формулы, не обязательно сложения или вычитания. И понятно, что для сложения используется символ «+», для вычитания символ «-».

Сложные варианты сложения: Функция СУММ()

Одним из сложных вариантов является прибавление процентов. Из-за сложности вопроса я написал отдельную статью.

КАК ПРИБАВИТЬ ПРОЦЕНТЫ В EXCEL С ПОМОЩЬЮ ФОРМУЛЫ

Прежде всего, нужно рассмотреть сложение ячеек по столбцу. Наилучший способ использование в формуле функции «СУММ». Этой функции передается диапазон ячеек и/или указываются, через точку с запятой, ячейки, по которым нужно провести суммирование.

Вид задания

Посмотрите на рисунок, условия задачи таковы: в ячейку F6 нужно записать сумму чисел записанных в диапазоне С1:С5, прибавить D1 и прибавить диапазон чисел записанный в D3:D5.

1. Становимся курсором в позицию F6 и нажимаем на кнопку «Вставить функцию».
2. В открывшемся окне «Мастер функций», есть поле поиск функции , в него мы записываем «Сумм»(без кавычек) и нажимаем кнопку «Ок»(в диалоговом окне)!

Мастер функций

После проделанных действий откроется другое диалоговое окно «Аргументы функции».

Теперь для функции сумм нужно установить параметры – диапазоны и ячейки для суммирования

Обращаю внимание, что таких параметров может быть 255 и при ручном вводе разделять их нужно символом «;»

Аргументы функций

После нажатия на кнопке , в ячейке F6 будет записана формула содержащая функцию суммирования, но пользователь увидит результат суммирования.

Думаю, прочитав эту статью, вы убедились, что операции сложения и вычитания это очень просто. Могу лишь посоветовать экспериментировать, экспериментировать и еще …

Сложение и вычитание матриц в Excel

Способ 1

Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С
будет равен сумме соответствующих элементов матриц А
и В
, т.е. с ij
= а ij
+ b
ij
.

Рассмотрим матрицы А
и В
размерностью 3х4
. Вычислим сумму этих матриц. Для этого в ячейку N
3
введем формулу =B3+H3
, где B3
и H3
— первые элементы матриц А
и В
соответственно. При этом формула содержит относительные ссылки (В3
и H
3
), чтобы при копировании формулы на весь диапазон матрицы С
они могли измениться.

С помощью маркера автозаполнения скопируем формулу из ячейки N
3
вниз и вправо на весь диапазон матрицы С
.

Для вычитания матрицы В
из матрицы А
(С=А — В
) в ячейку N
3
введем формулу =B3 — H3
и скопируем её на весь диапазон матрицы С
.

Способ 2

Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А
, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В
. После ввода формулы нажимаем сочетание клавиш Ctrl+
Shift+
Enter
, чтобы значениями заполнился весь диапазон.

Вычисление обратной матрицы в MS EXCEL

Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() или англ. MINVERSE.

• Понятие обратной матрицы определено только для квадратных матриц, определитель которых отличен от нуля.
• СОВЕТ: О нахождении определителя матрицы читайте статью Вычисление определителя матрицы в MS EXCEL
• Матрица А-1 называется обратной для исходной матрицы А порядка n, если справедливы равенства А-1*А=Е и А*А-1=Е, где Е единичная матрица порядка n.
• Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР().

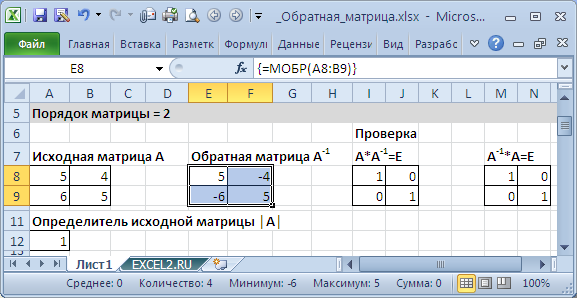
Если элементы исходной матрицы 2 х 2 расположены в диапазоне А8:В9, то для получения транспонированной матрицы нужно (см. файл примера):

• выделить диапазон 2 х 2, который не пересекается с исходным диапазоном А8:В9, например, Е8:F9
• в Cтроке формул ввести формулу =МОБР(A8:B9) и нажать комбинацию клавиш CTRL+SHIFT+ENTER, т.е. нужно ввести ее как формулу массива (формулу можно ввести прямо в ячейку, предварительно нажав клавишу F2)

Если матрица большей размерности, то перед вводом формулы нужно выделить соответственно больший диапазон ячеек.

Массив может быть задан не только как интервал ячеек, например A8:B9, но и как массив констант, например =МОБР({5;4: 3;2}).

Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией.

Ссылка на массив также может быть указана как ссылка на именованный диапазон.

Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция МОБР() возвращает значение ошибки #ЧИСЛО!. Матрицы не могут быть обращены, у которых определитель равен 0.

Если функция МОБР() вернула значение ошибки #ЗНАЧ!, то либо число строк в массиве не равно числу столбцов, либо какая-либо из ячеек в массиве пуста или содержит текст. Т.е. функция МОБР() пустую ячейку воспринимает не как содержащую 0 (как например, это делает СУММ()), а как ошибочное значение.

Вычисление обратной матрицы с помощью матрицы из алгебраических дополнений

СОВЕТ: Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция МОБР().

В файле примера приведен расчет обратной матрицы 3-го порядка через матрицу алгебраических дополнений.

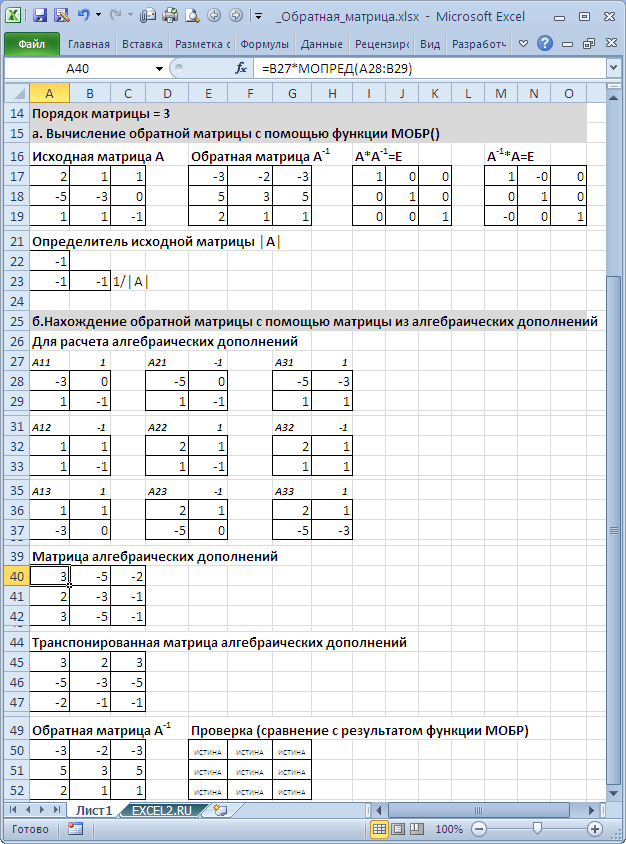
В качестве проверки можно перемножить исходную и обратную матрицы. В результате должна получиться единичная матрица.

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
2. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
3. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
4. Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
2. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
3. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
4. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
5. Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

На этом расчет можно считать завершенным.

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Нахождение обратной матрицы всегда вызывало большие затруднения у учащихся, так как это был очень трудоемкий процесс. И вот такое задание вполне по силам EXCEL.  

Прежде всего, уясним одно правило:  Матрица имеет обратную только тогда, когда ее определитель не равен нулю.  А вот и задание: найдите матрицу, обратную к матрице А, где

Вычислять определитель этой матрицы мы умеем. Я его уже вычислил.

Он оказался равен -4, а  это значит, что у нашей матрицы есть обратная (если бы определитель оказался равен нулю, то мы сказали бы что матрица не имеет обратную и немедленно прекратили все вычисления). Теперь отметим ячейку, с которой начнем записывать ответ. Я отметил ячейку E1.  Нажимаем Формулы, затем Математические и в появившемся окне находим  МОБР

После нажатия появляется вот такое окно, в котором надо вписать адреса ячеек, в которых находятся элементы матрицы  в Массив

У нас элементы записаны в ячейки начиная с А1 и заканчивая в С3 , поэтому так и записываем (смотрите картинку)

Если все сделали правильно, то автоматически заполнится место, обведенное красным и запишется ответ, который обведен черным. В таком виде ответ трудно переваривать и поэтому нажимаем ОК.  В ячейке, которую мы застолбили под ответ, появилось число 3,  Это только первый элемент полученной обратной матрицы.

Чтобы виден был весь ответ, выполняем следующие действия: Начиная с  ячейки Е1 выделяем три строчки и три столбца (именно столько было у исходной матрицы и столько же будет у обратной)

нажимаем клавишу F2,  а затем на одновременно на три клавиши  Ctrl+Shift+Enter.

В выделенном месте появляются, теперь уже все, элементы обратной матрицы. Если Вы сохраните этот документ, то в следующий раз можете воспользоваться плодами своего труда. Так, меняя элементы исходной матрицы, Вы автоматически получаете для нее же обратную матрицу.

На этом все. Крепких вам знаний.

Рубрика: EXCEL в помощь, Статьи. Метки: EXCEL, ИКТ, матрица, обратная матрица

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

2.8. Критическая ошибка в Excel 2003

В Excel 2003 функции TREND и
LINEST при определенных
условиях дают неверный результат.

Так происходит когда одновременно:

• среднее значение по каждой переменной в матрице
  предикторов X равно нулю;

• среднее значение отклика Y
  не равно нулю.

На показан как раз такой
случай: средние значения по всем столбцам матрицы Xc
равны нулю, а среднее по столбцу Yc отлично от нуля..

Пример 
 

Рис.37 Ошибка в регрессионных функциях Excel
2003

Ситуацию можно исправить, применяя функцию
TREND к
центрированным значениям отклика, с последующей коррекцией результата.
Для этого можно использовать формулу
=TREND(Yc-ym,
Xc)+ym, применение которой показано на том же рисунке.

Удивительно, но эта ошибка не была замечена
пользователями. Однако в новой версии 2007 она исправлена.